Cho hình hộp chữ nhật ABCDA'B'C'D' có AD = 6cm, A'B' = 4cm, CC' = 3,5cm.
a) Tính độ dài các cạnh còn lại của hình hộp chữ nhật.
b) Tính độ dài đoạn BD. Tính Sxq, Stp và V của hình hộp này.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định lí Py-ta-go vào \(\Delta ABC\), ta được : \(BC=\sqrt{5^2-4^2}=3cm\)
Từ định nghĩa của hình hộp Chữ nhật ta có :
\(AA_1\perp\left(ABCD\right)\Rightarrow AA_1\perp AC\)
\(\Leftrightarrow\Delta A_1AC\)vuông tại A
Áp dụng định lý Py-ta-go vào \(\Delta A_1AC\), ta được : \(AA_1=\sqrt{13^2-5^2}=12cm\)
=> Diện tích xung quanh hình hộp chữ nhật đó là : \(2\left(AB+BC\right)\cdot AA_1=2\left(4+3\right)\cdot12=168\left(cm^2\right)\)
Diện tích toàn phần của hình hộp chữ nhật là : \(168+2.4.3=192\left(cm^2\right)\)
Thể tích toàn phần của hình hộp chữ nhật là : \(AB.BC.AA_1=4.3.12=144\left(cm^3\right)\)
KL : ............

a: ΔHBA\(\sim\)ΔABC
ΔHAC\(\sim\)ΔABC
ΔHBA\(\sim\)ΔHAC
b: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/3=DC/4
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{10}{7}\)
Do đo: DB=30/7cm; DC=40/7cm
c: Xét ΔBAC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\)

Đáp án B
Ta có: A C = A B 2 + B C 2 = a 5
Bán kính mặt cầu ngoại tiếp là 3 a 2 ⇒ A C ' = 3 a
Xét tam giác A C C ' vuông tại C, ta có: C C ' = A C ' 2 - A C 2 = 2 a
Thể tích hình hộp là:
V = C C ' . S A B C D = 2 a . a . 2 a = 4 a 3

a) Tên 5 đỉnh: M, N, F, E, P
Tên 4 mặt: MNEF, MNQP, PQGH, NEGQ.
Lưu ý: HS có thể liệt kê tên các đỉnh, các mặt khác.
b) Tên các cạnh: MN, NE, EF, FM, PQ, QG, GH, HP, MP, FH, NQ, EG
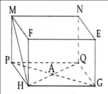
a: BC=C'B'=A'D'=6cm
AB=CD=D'C'=4cm
D'D=A'A=BB'=3,5cm
b: \(BD=\sqrt{6^2+4^2}=2\sqrt{13}\left(cm\right)\)
S xq=(6+4)*2*3,5=7*10=70cm2
STp=70+2*6*4=118cm2
V=6*4*3,5=14*6=84cm3