Tìm min hoặc max của 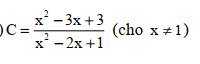
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài này tìm được min thôi
Ta có: \(2x^2+x=2\left(x^2+\frac{1}{2}x+\frac{1}{16}\right)-\frac{1}{8}=2\left(x+\frac{1}{4}\right)^2-\frac{1}{8}\ge-\frac{1}{8}\left(\forall x\right)\)
Dấu "=" xảy ra khi: \(2\left(x+\frac{1}{4}\right)^2=0\Rightarrow x=-\frac{1}{4}\)
Vậy Min = -1/8 khi x = -1/4

\(D=\dfrac{21}{\left|x-2\right|+3}\le\dfrac{21}{3}=7\forall x\)
Dấu '=' xảy ra khi x=2

\(C=2x^2+y^2-2xy-2y+5\)
\(\Rightarrow2C=4x^2+2y^2-4xy-4y-10\)
\(2C=\left(2x\right)^2-2.2x.y+y^2+y^2-4y+4-14\)
\(2C=\left(2x-y\right)^2+\left(y-2\right)^2-14\)
Với mọi x, y ta có: \(\left(2x-y\right)^2\ge0;\left(y-2\right)^2\ge0\)
\(\Rightarrow\left(2x-y\right)^2+\left(y-2\right)^2\ge0\)
\(\Rightarrow2C=\left(2x-y\right)^2+\left(y-2\right)^2-14\ge-14\)
\(\Rightarrow C\ge\frac{-14}{2}=-7\)
Dấu bằng xảy ra khi: \(\hept{\begin{cases}2x-y=0\\y-2=0\end{cases}\Leftrightarrow\hept{\begin{cases}2x=y\\y=2\end{cases}\Leftrightarrow}\hept{\begin{cases}2x=2\\y=2\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=2\end{cases}}}\)
Vậy x=1 ; y=2 thì min C = -7
HỌC TỐT <3

\(F=\sqrt{-3x^2-6x+2}\left(Đk:-1-\sqrt{\dfrac{5}{3}}\le x\le\sqrt{\dfrac{5}{3}}-1\right)\)
\(=\sqrt{-\left(3x^2+6x+3\right)+5}\)
\(=\sqrt{-3\left(x+1\right)^2+5}\)
Vì \(-\left(x+1\right)^2\le0\forall x\)
\(\Rightarrow F\le\sqrt{5}\)
\(MaxF=\sqrt{5}\Leftrightarrow x=-1\)

Ta có: \(\left\{{}\begin{matrix}\left(x-3\right)^2\ge0\forall x\\\left|y-5\right|\ge0\forall y\end{matrix}\right.\)
\(\Rightarrow\left(x-3\right)^2+\left|y-5\right|\ge0\forall x,y\)
\(\Rightarrow10+\left(x-3\right)^2+\left|y-5\right|\ge10\forall x,y\)
\(\Rightarrow D=-10-\left(x-3\right)^2-\left|y-5\right|\le-10\forall x,y\)
Dấu \("="\) xảy ra khi: \(\left\{{}\begin{matrix}x-3=0\\y-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=5\end{matrix}\right.\)
Vậy \(Max_D=-10\) khi \(x=3;y=5\).

\(A=\left|x-3\right|+\left|5-x\right|+\left|x+2\right|-4\ge\left|x-3\right|+\left|5-x+x+2\right|-4\)
\(A\ge\left|x-3\right|+3\ge3\)
\(A_{min}=3\) khi \(x=3\)

Với mọi a;b ta có: \(\left(a-b\right)^2\ge0\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Leftrightarrow a^2+b^2\ge2ab\Leftrightarrow2a^2+2b^2\ge a^2+2ab+b^2\)
\(\Leftrightarrow a^2+b^2\ge\dfrac{1}{2}\left(a+b\right)^2\)
Dấu "=" xảy ra khi và chỉ khi \(a=b\)
Áp dụng:
\(A=\left(x+3\right)^4+\left(7-x\right)^4\ge\dfrac{1}{2}\left[\left(x+3\right)^2+\left(7-x\right)^2\right]^2\)
Tiếp tục áp dụng BĐT ban đầu trong 2 số hạng trong ngoặc vuông:
\(\Rightarrow A\ge\dfrac{1}{2}\left[\dfrac{1}{2}\left(x+3+7-x\right)^2\right]^2=1250\)
Dấu "=" xảy ra khi \(x+3=7-x\Rightarrow x=2\)
Vậy \(A_{min}=1250\) khi \(x=2\)
Không tồn tại A max
Lời giải:
$C=\frac{x^2-3x+3}{x^2-2x+1}$
$\Rightarrow C(x^2-2x+1)=x^2-3x+3$
$\Leftrightarrow x^2(C-1)+x(3-2C)+(C-3)=0(*)$
Coi $(*)$ là pt bậc 2 ẩn $x$. Vì $C$ tồn tại nên $(*)$ có nghiệm.
$\Leftrightarrow \Delta'=(3-2C)^2-4(C-3)(C-1)\geq 0$
$\Leftrightarrow 4C-3\geq 0$
$\Leftrightarrow C\geq \frac{3}{4}$
Vậy $C_{\min}=\frac{3}{4}$