CMR nếu tổng các số x, y, z không âm thì : x3+ y3+ z3 lớn hơn hoặc bằng 3xyz
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 10 2017
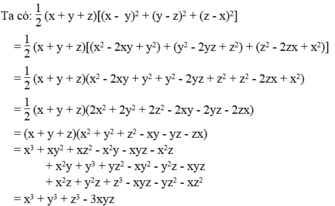
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Nếu x ≥ 0, y ≥ 0, z ≥ 0 thì:
x + y + z ≥ 0
x - y 2 + y - z 2 + z - x 2 ≥ 0
Suy ra:
x 3 + y 3 + z 3 - 3 x y z ≥ 0 ⇔ x 3 + y 3 + z 3 ≥ 3 x y z
Hay: x 3 + y 3 + z 3 3 ≥ x y z
CM
19 tháng 11 2018
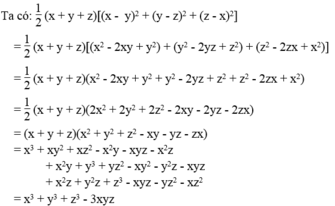
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Nếu a ≥ 0, b ≥ 0, c ≥ 0 thì :
16 tháng 5 2023
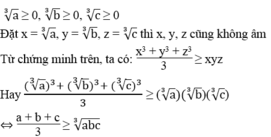
a: =(x+y)^3+z^3-3xy(x+y)-3xyz
=(x+y+z)(x^2+2xy+y^2-xz-yz+z^2)-3xy(x+y+z)
=(x+y+z)(x^2+y^2+z^2-xy-xz-yz)
b: a+b+c<>0
A=(a+b+c)^3-a^3-b^3-c^3/a+b+c
=(a+b+c)(a^2+b^2+c^2-ab-ac-bc)/(a+b+c)
=a^2+b^2+c^2-ab-ac-bc
=1/2[a^2-2ab+b^2+b^2-2bc+c^2+a^2-2ac+c^2]
=1/2[(a-b)^2+(b-c)^2+(a-c)^2]>=0
QT
1
9 tháng 7 2020
Ta có: \(x^3+y^3+z^3-3xyz\)
\(=\left(x+y\right)^3-3xy\left(x+y\right)+z^3-3xyz\)
\(=\left[\left(x+y\right)^3+z^3\right]-\left[3xy\left(x+y\right)+3xyz\right]\)
\(=\left(x+y+z\right)\left[\left(x+y\right)^2-z\left(x+y\right)+z^2\right]-\left[3xy\left(x+y+z\right)\right]\)
\(=\left(x+y+z\right)\left(x^2+2xy+y^2-zx-zy+z^2\right)-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left(x^2+2xy+y^2-zx-zy+z^2-3xy\right)\)
\(=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)\)(đpcm)
NA
1
26 tháng 2 2020
Ta rút gọn tử thức trc: \(x^3+y^3+z^3-3xyz=x^3+y^3+z^3+x^2y-x^2y+xy^2-xy^2+y^2z-y^2z+yz^2-yz^2+x^2z-x^2z+xz^2-xz^2-xyz-xyz-xyz=x^2\left(x+y+z\right)+y^2\left(x+y+z\right)+z^2\left(x+y+z\right)-x\left(x+y+z\right)-yz\left(x+y+z\right)-xz\left(x+y+z\right)=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)=\frac{1}{2}\left(x+y+z\right)\left(x^2-2xy+y^2+y^2-2yz+z^2+z^2-2xz+x^2\right)=\frac{1}{2}\left(x+y+z\right)\left(\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\right)\)tới đây rút gọn đc rồi chứ
N
1
27 tháng 10 2021
\(x^3+y^3+z^3-3xyz=0\)
\(\Leftrightarrow\left(x+y\right)^3+z^3-3xy\left(x+y\right)-3xyz=0\)
\(\Leftrightarrow\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2-3xy\right)=0\)
\(\Leftrightarrow x^2+y^2+z^2-xy-xz-yz=0\)
\(\Leftrightarrow x=y=z\)
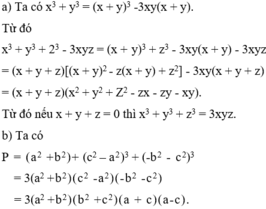
AM-GM 3 số
chết mk nhìn nhầm , tổng ko âm chứ ko phải x,y,z ko âm