Điền số hạng còn thiếu trong dãy số sau:1;2;5;10;17;26;...;50;65 Điền số hạng còn thiếu trong dãy số sau: 6;13;21;30;.... Cần lời giải chi tiết ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PQ
6
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 6 2023
Dãy số trên là dãy số cách đều với khoảng cách là:
93 109 - 93 009 = 100
Vậy số tiếp theo cần điền vào chỗ còn thiếu là:
93 109 + 100 = 93 209
Đáp số: 93 209
8 tháng 6 2023
Dãy số trên là dãy số cách đều với khoảng cách là:
93 109 - 93 009 = 100
Vậy số tiếp theo cần điền vào chỗ còn thiếu là:
93 109 + 100 = 93 209
Đáp số: 93 209
KN
0
LT
1
24 tháng 8 2021
a. 7, 10, 13,16, 19, 22, 25.
b. 103, 95, 87,79, 71, 63, 55, 47.
18 tháng 3 2017
tôi nghĩ bài các bạn sẽ làm ngon ơ aingowf các bạn ko làm đc,tôi là một lập trình viên thật sự đấy
LN
3
4 tháng 8 2016
Ta thấy rằng:
\(\frac{1}{2}=\frac{1}{1.2}\)
\(\frac{1}{6}=\frac{1}{2.3}\)
\(\frac{1}{12}=\frac{1}{3.4}\)
\(\frac{1}{20}=\frac{1}{4.5}\)
\(\frac{1}{30}=\frac{1}{5.6}\)
Vậy số hạng cần tìm = \(\frac{1}{6.7}=\frac{1}{42}\)
Đáp số: \(\frac{1}{42}\)
NT
1
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
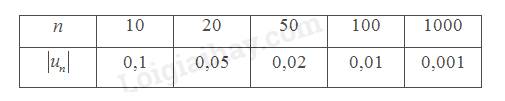
a) \(n = 100 \Leftrightarrow \left| {{u_{100}}} \right| = \left| {\frac{{{{\left( { - 1} \right)}^{100}}}}{{100}}} \right| = \frac{1}{{100}} = 0,01\)
\(n = 1000 \Leftrightarrow \left| {{u_{1000}}} \right| = \left| {\frac{{{{\left( { - 1} \right)}^{1000}}}}{{1000}}} \right| = \frac{1}{{1000}} = 0,001\)
Như vậy ta có thể điền vào bảng như sau:
b) \(\left| {{u_n}} \right| < 0,01 \Leftrightarrow \left| {\frac{{{{\left( { - 1} \right)}^n}}}{n}} \right| < 0,01 \Leftrightarrow \frac{1}{n} < 0,01 \Leftrightarrow n > 100\)
Vậy \(\left| {{u_n}} \right| < 0,01\) khi \(n > 100\).
\(\left| {{u_n}} \right| < 0,001 \Leftrightarrow \left| {\frac{{{{\left( { - 1} \right)}^n}}}{n}} \right| < 0,001 \Leftrightarrow \frac{1}{n} < 0,001 \Leftrightarrow n > 1000\)
Vậy \(\left| {{u_n}} \right| < 0,001\) khi \(n > 1000\).
c) Dựa vào trục số ta thấy, khoảng cách từ điểm \({u_n}\) đến điểm 0 trở nên rất bé khi \(n\) trở nên rất lớn.
37
40
37
40