giúp mình bài 3 và bài 6 với cảm ơn ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




mình làm những bài bn chưa lm nhé
9B
10A
bài 2
have repainted
bàii 3
ride - walikking
swimming
watch

Câu 5:
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
c: Xét tứ giác AEDF có
\(\widehat{EAF}=\widehat{AFD}=\widehat{AED}=90^0\)
Do đó: AEDF là hình chữ nhật
mà AD là tia phân giác của \(\widehat{FAE}\)
nên AEDF là hình vuông

Bài 6:
\(\sqrt{x^2-12x+36}=10\\ \sqrt{\left(x-6\right)^2}=10\\ \left|x-6\right|=10\\ x-6=10\\ x=10+6=16\)
6:
=>\(\sqrt{\left(x-6\right)^2}=10\)
=>|x-6|=10
=>x-6=10 hoặc x-6=-10
=>x=16 hoặc x=-4


Câu 4:
D và F cùng nhìn AC dưới 1 góc vuông nên tứ giác ACDF nội tiếp
\(\Rightarrow\widehat{ADF}=\widehat{ACF}\) (cùng chắn AF)
Tương tự, ABDE nội tiếp \(\Rightarrow\widehat{ABE}=\widehat{ADE}\) (cùng chắn AE)
Lại có \(\widehat{ABE}=\widehat{ACF}\) (cùng phụ góc \(\widehat{A}\))
\(\Rightarrow\widehat{ADE}=\widehat{ADF}\) hay AD là phân giác góc \(\widehat{FDE}\)
./
Hoàn toàn tương tự, ta cũng có CF là phân giác \(\widehat{DFE}\Rightarrow\widehat{BFD}=\widehat{AFE}\)
Mà \(\widehat{AFE}=\widehat{BFK}\Rightarrow\widehat{BFK}=\widehat{BFD}\)
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{FK}{FD}\) theo định lý phân giác
Đồng thời \(\dfrac{CK}{CD}=\dfrac{FK}{FD}\) (CF là phân giác ngoài góc \(\widehat{DFK}\))
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{CK}{CD}\Rightarrow\dfrac{BK}{CK}=\dfrac{BD}{CD}\)
Qua B kẻ đường thẳng song song AC cắt AK và AD tại P và Q
Theo Talet: \(\dfrac{BK}{CK}=\dfrac{BP}{AC}\) đồng thời \(\dfrac{BD}{DC}=\dfrac{BQ}{AC}\)
\(\Rightarrow\dfrac{BP}{AC}=\dfrac{BQ}{AC}\Rightarrow BP=BQ\)
Mặt khác BP song song MF (cùng song song AC)
\(\Rightarrow\dfrac{MF}{BP}=\dfrac{AF}{AB}\) ; \(\dfrac{NF}{BQ}=\dfrac{AF}{AB}\) (Talet)
\(\Rightarrow\dfrac{MF}{BP}=\dfrac{NF}{BQ}\Rightarrow MF=NF\)

12: Gọi vận tốc lúc về là x
Theo đề, ta có: x/60=1:0,8=5/4
=>x=75
11:
b: k=xy=4,5
Khi y=-0,5 thì x=4,5/-0,5=-9
c: v2*t2=v1*t1
=>t2/t1=v1/v2=5/6
d: Chiều dài và chiều rộng là hai đại lượng tỉ lệ nghịch
=>Nếu tăng chiều dài lên a lần và muốn giữ nguyên diện tích thì cần giảm chiều rộng đi a lần






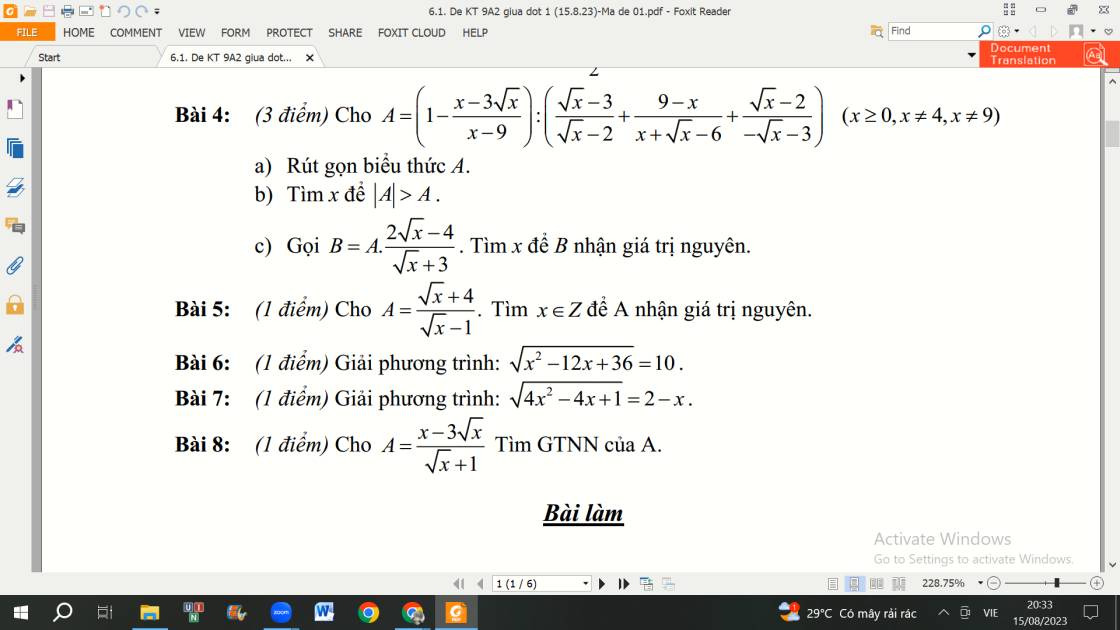








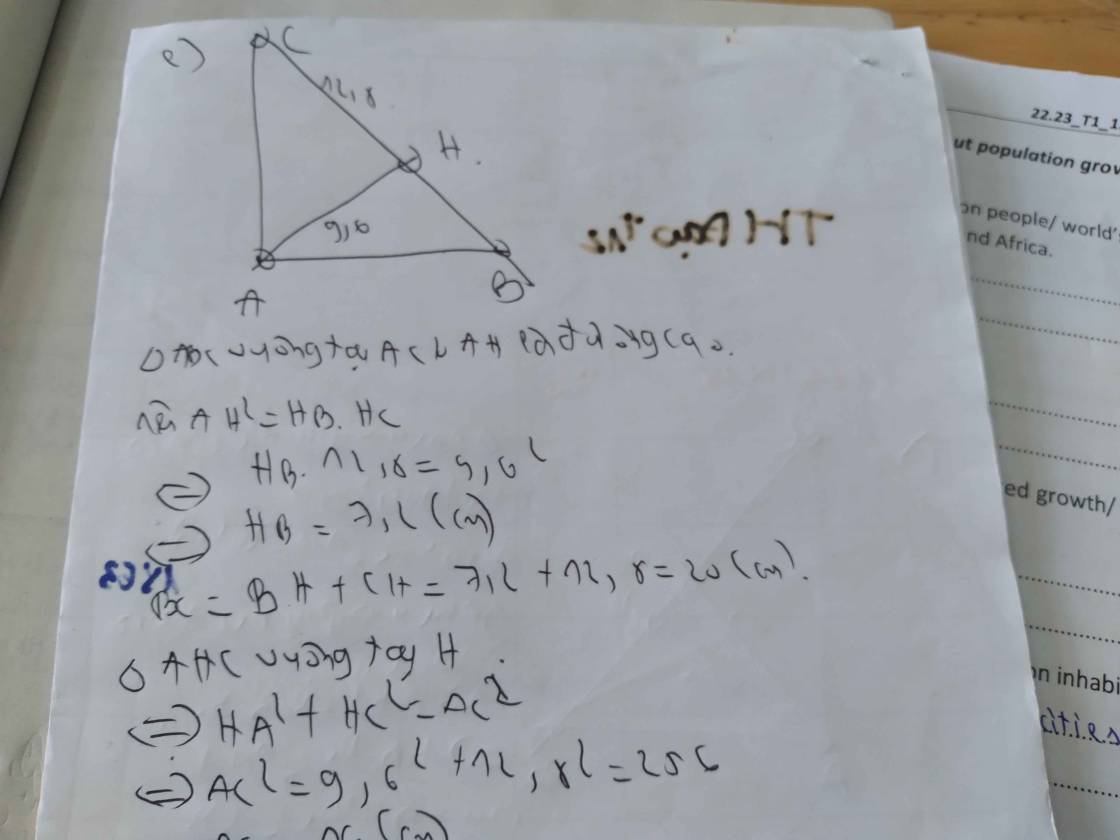

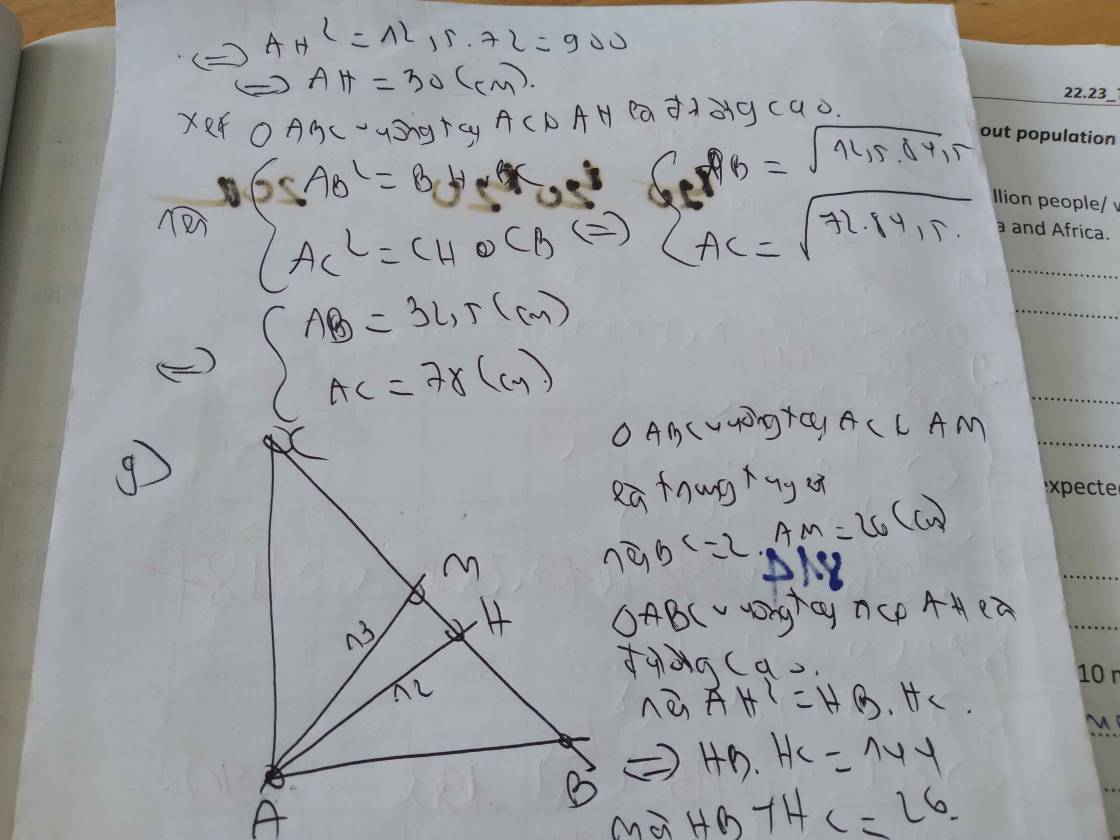

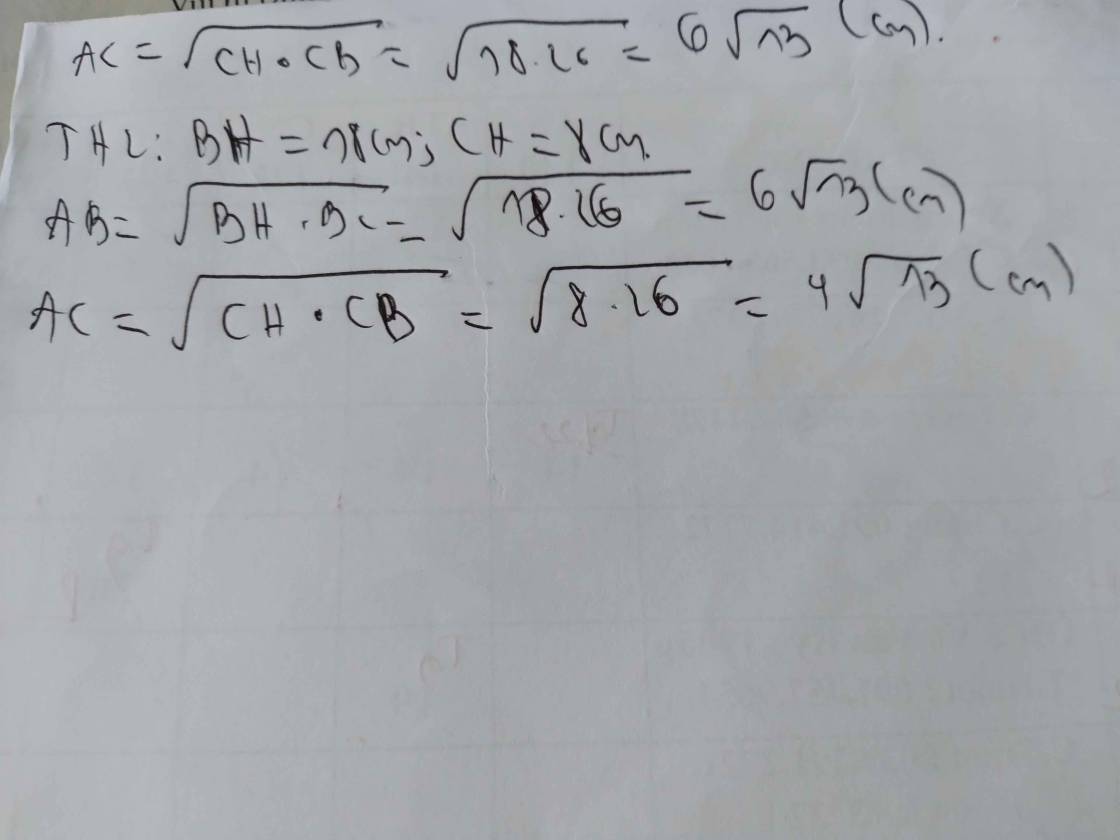


 giúp mình 3 bài trên với ạ! mình cảm ơn
giúp mình 3 bài trên với ạ! mình cảm ơn