Chứng minh tích hai trung tỉ bằng hai ngoại tỉ nếu \(\frac{a}{b}=\frac{c}{d}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 10 2016
Đặt \(\frac{a}{b}=\frac{c}{d}=k\)\(\Rightarrow a=bk;c=dk\)
a)Xét \(VT=\frac{2a+3b}{2a-3b}=\frac{2bk+3b}{2bk-3b}=\frac{b\left(2k+3\right)}{b\left(2k-3\right)}=\frac{2k+3}{2k-3}\left(1\right)\)
Xét \(VP=\frac{2c+3d}{2c-3d}=\frac{2dk+3d}{2dk-3d}=\frac{d\left(2k+3\right)}{d\left(2k-3\right)}=\frac{2k+3}{2k-3}\left(2\right)\)
Từ (1) và (2) =>Đpcm
b)Xét \(VT=\frac{ab}{cd}=\frac{bkb}{dkd}=\frac{b^2k}{d^2k}=\frac{b^2}{d^2}\left(1\right)\)
Xét \(VP=\frac{\left(bk\right)^2+b^2}{\left(dk\right)^2+d^2}=\frac{b^2k^2+b^2}{d^2k^2+d^2}=\frac{b^2\left(k+1\right)}{d^2\left(k+1\right)}=\frac{b^2}{d^2}\left(2\right)\)
Từ (1) và (2) =>Đpcm
c)Xét \(VT=\left(\frac{a+b}{c+d}\right)^2=\left(\frac{bk+b}{dk+d}\right)^2=\left[\frac{b\left(k+1\right)}{d\left(k+1\right)}\right]^2=\left[\frac{b}{d}\right]^2=\frac{b^2}{d^2}\left(1\right)\)
Xét \(VP=\frac{a^2+b^2}{c^2+d^2}=\frac{\left(bk\right)^2+b^2}{\left(dk\right)^2+d^2}=\frac{b^2k^2+b^2}{d^2k^2+d^2}=\frac{b^2\left(k+1\right)}{d^2\left(k+1\right)}=\frac{b^2}{d^2}\left(2\right)\)
Từ (1) và (2) =>Đpcm
T
22 tháng 10 2016
a/ theo bài ra, ta có:
\(\frac{a}{b}=\frac{c}{d}\\ \Rightarrow\frac{a}{c}=\frac{b}{d}\\ \Rightarrow\frac{2a}{2c}=\frac{3b}{3d}\)
áp dụng tính caahts dã y tỉ số bằng nhau ta có :
\(\frac{2a}{2c}=\frac{3b}{3d}=\frac{2a+3b}{2c+3d}=\frac{2a-3b}{2c-3d}\)
=> \(\frac{2a+3b}{2c+3d}=\frac{2a-3b}{2c-3d}\\ \Rightarrow\frac{2a+3b}{2a-3b}=\frac{2c+3d}{2c-3d}\left(đpcm\right)\)
b/ theo bài ra, ta có:
\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\\ \Rightarrow\left(\frac{a}{c}\right)^2=\left(\frac{b}{d}\right)^2=\frac{ab}{cd}\left(1\right)\)
ta có:
\(\left(\frac{a}{c}\right)^2=\left(\frac{b}{d}\right)^2=\frac{a^2}{c^2}=\frac{b^2}{d^2}\)
=> \(\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{a^2-b^2}{c^2-d^2}\) (2)
từ 1 và 2 => đpcm
c/ theo bài ra, ta có:
\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\)
đặt \(\frac{a}{c}=\frac{b}{d}=k\)
ta có: a = kc
b = kd
=> \(\left(\frac{a+b}{c+d}\right)^2=\left(\frac{kc+kd}{c+d}\right)^2=\left(\frac{k\left(c+d\right)}{c+d}\right)^2=k^2\) (1)
=> \(\frac{a^2+b^2}{c^2+d^2}=\frac{\left(kc\right)^2+\left(kd\right)^2}{c^2+d^2}=\frac{k^2c^2+k^2d^2}{c^2+d^2}=\frac{k^2\left(c^2+d^2\right)}{c^2+d^2}=k^2\left(2\right)\)
từ 1 và 2 => đpcm
N3
9 tháng 4 2019
Nhận xét : Nếu hai vế của mỗi đẳng thức < vế phải , vế trái của dấu '='> cùng thêm hay bớt cùng một số thì giá trị hai vế của đặng thức vẫn không thay đổi
Ta Có : \(\frac{a}{b}\)= \(\frac{c}{d}\)=> ad = bc ( theo kết quả trên )
Cộng hai vế của đẳng thức trên với ab ta được
ad + ab = bn + ab
Áp dụng tính chất phân phối của phép nhân đối vói phép công ta được :
a( d + b ) = b( a + c ) => \(\frac{a}{b}\)=\(\frac{a+c}{b+d}\) ( 1 )
Tương tự : \(\frac{a}{b}\)= \(\frac{c}{d}\)=> ad = bc
Cộng hai vế của đẳng thức trên với cd ta được :
ad + cd = bc + cd
d( a + c ) = c( b +d )
\(\frac{c}{d}\) = \(\frac{a+c}{b+d}\) ( 2 )
Từ (1) và (2) có : \(\frac{a}{b}\)= \(\frac{c}{d}\)= \(\frac{a+c}{b+d}\)
KN
9 tháng 4 2019
Sửa lại đề tí nhá :v
Chứng minh dãy tỉ số bằng nhau : Nếu \(\frac{a}{b}=\frac{c}{d}\)thì \(\frac{a+c}{b+d}=\frac{a-c}{b-d}\).
Giải :
Đặt \(\frac{a}{b}=\frac{c}{d}=k\)
=> \(a=b.k;c=d.k\)
=> \(a+c=b.k+d.k\)
=> \(a+c=k.\left(b+d\right)\)
=> \(\frac{a+c}{b+d}=k\)và \(\frac{a-c}{b-d}=k\left(đpcm\right)\)
HQ
Hà Quang Minh
Giáo viên
16 tháng 9 2023
a) Ta có: 6. (-15) = -90;
10.(-9) = = - 90
Vậy tích hai số hạng 6 và -15 bằng tích hai số hạng 10 và -9
b) Nhân hai vế của tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\) với tích bd, ta được: \(\frac{{a.b.d}}{b} = \frac{{c.b.d}}{d} \Rightarrow ad = bc\)
Vậy ta được đẳng thức ad = bc
KV
16 tháng 9 2023
a) 6.(-15) = 10.(-9) = -90
b) a/b . bd = ad
c/d . bd = bc
Ta được ad = bc
HT
17 tháng 6 2016
- Chứng minh thuận:
Nhân 2 vế của a/b với d, nhân 2 vế của c/d với b rồi so sánh
- Chứng minh đảo: Hơi khó giải thích...
Cộng ad với bd và bc với bd....
18 tháng 6 2016
Có gì mà loằng ngoằng vậy.
1./ Thuận: Nếu: \(\frac{a}{b}>\frac{c}{d}\)nhân cả 2 vế BĐT với tích bd >0 (vì b>0; d>0) BĐT không đổi chiều, ta có: \(\frac{a}{b}\cdot bd>\frac{c}{d}\cdot bd\Rightarrow a\cdot d>b\cdot c\)đpcm
2./ Nghịch: Nếu \(a\cdot d>b\cdot c\)chia cả 2 vế BĐT với tích bd >0 (vì b>0; d>0) BĐT không đổi chiều, ta có: \(\frac{a\cdot d}{b\cdot d}>\frac{b\cdot c}{b\cdot d}\Rightarrow\frac{a}{b}>\frac{c}{d}\)đpcm
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
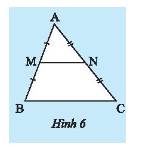
a) Vì \(AM = MB \Rightarrow M\) là trung điểm của \(AB\) (do \(M\) thuộc \(AB\))
\( \Rightarrow AM = \frac{1}{2}AB \Leftrightarrow \frac{{AM}}{{AB}} = \frac{1}{2}\);
Vì \(AN = NC \Rightarrow N\) là trung điểm của \(AC\) (do \(N\) thuộc \(AC\))
\( \Rightarrow AN = \frac{1}{2}AC \Leftrightarrow \frac{{AN}}{{AC}} = \frac{1}{2}\).
b) Vì \(\frac{{AM}}{{AB}} = \frac{1}{2};\frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\).
Xét tam giác \(ABC\) có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) nên áp dụng định lí Thales đảo ta được \(MN//BC\).
c) Xét tam giác \(ABC\) có \(MN//BC\) nên áp dụng hệ quả định lí Thales ta được \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\)
Mà \(\frac{{AM}}{{AB}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\).
Vậy \(\frac{{MN}}{{BC}} = \frac{1}{2}\) (điều phải chứng minh).
21 tháng 6 2017
- Ta có trên trục số 2 điểm A và B lần lượt là : \(\frac{a}{b},\frac{c}{d}\)
mà trên trục số \(\frac{a}{b}\)nằm bên trái \(\frac{c}{d}\)=) \(\frac{a}{b}< \frac{d}{c}\)
- Như ta đã biết : Nếu \(\frac{a}{b}< \frac{c}{d}\)=) \(\frac{a}{b}< \frac{a+c}{b+d}< \frac{c}{d}\)
- Mà kí hiệu \(\frac{a+c}{b+d}\)là C
Vậy ta luôn có \(C\)nằm giữa \(A,B\)=) Trên trục số,giữa 2 điểm biểu diễn 2 số hữu tỉ \(\frac{a}{b}\)và \(\frac{c}{d}\)luôn tồn tại 1 điểm biểu diễn số hữu tỉ khác ( ĐPCM )
DL
15 tháng 4 2020
có ai trả lời hộ mình câu hỏi này ở trong trang cá nhân của mình ko
16 tháng 6 2016
a) \(\frac{a}{b}< \frac{c}{d}\Leftrightarrow\frac{ad}{bd}< \frac{bc}{bd}\) (quy đồng mẫu chung)
Vì b,d > 0 nên bd > 0. Do đó ad < bc (đpcm)
b) ad < bc \(\Leftrightarrow\frac{ad}{bd}< \frac{bc}{bd}\) (cùng chia cho bd)
Vì b,d > 0 nên bd > 0. Do đó \(\frac{a}{b}< \frac{c}{d}\) (rút gọn tử và mẫu)
16 tháng 6 2016
a, Ta có: \(\frac{a}{b}< \frac{c}{d}\Rightarrow\frac{ad}{bd}< \frac{cb}{db}\Rightarrow ad< cb\)
b, Ta có: \(ad< bc\Rightarrow\frac{ad}{bd}< \frac{bc}{bd}\Rightarrow\frac{a}{b}< \frac{c}{d}\)
mk nha