Cho tam giác ABC Có phân giác BD = phân giác CE. CM tam giác ABC cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
K
cho tam giác abc góc a = 60 . phân giác bd và ce cắt nhau tại o . cm tam giác ode cân , BE + CD = BC
0
25 tháng 2 2022
-Xét △ABC có: BD, CE lần lượt là các đường phân giác (gt)
\(\Rightarrow\dfrac{BE}{AE}=\dfrac{BC}{AC};\dfrac{DC}{AD}=\dfrac{BC}{AB}\) (định lí đường phân giác trong tam giác)
Mà \(AB=AC\) (△ABC cân tại A)
\(\Rightarrow\dfrac{BE}{AE}=\dfrac{DC}{AD}\) nên DE//BC (định lí Ta-let đảo)
\(\Rightarrow\dfrac{AB}{AE}=\dfrac{BC}{DE}=\dfrac{8}{5}\) (định lí Ta-let)
\(\Rightarrow\dfrac{AB}{AE}-1=\dfrac{8}{5}-1\)
\(\Rightarrow\dfrac{BE}{AE}=\dfrac{3}{5}\) mà \(\dfrac{BE}{AE}=\dfrac{BC}{AC}\left(cmt\right)\)
\(\Rightarrow\dfrac{BC}{AC}=\dfrac{3}{5}\)
\(\Rightarrow AC=AB=\dfrac{5.BC}{3}=\dfrac{5.8}{3}=\dfrac{40}{3}\left(cm\right)\)
NM
2
12 tháng 3 2023
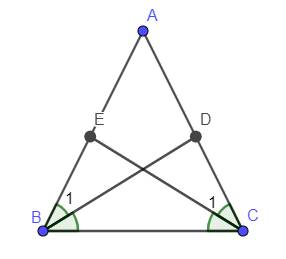
Có `Delta ABC` cân tại `A=>AB=AC;hat(ABC)=hat(ACB)`
Có `hat(ABC)=hat(ACB)(cmt)`
mà `BD` là p/g `hat(ABC)`
`CE` là p/g `hat(ACB)`
nên `hat(B_1)=hat(C_1)`
Xét `Delta ABD` và `Delta ACE` có :
`{:(hat(B_1)=hat(C_1)(cmt)),(AB=AC(cmt)),(hat(A)-chung):}}`
`=>Delta ABD=Delta ACE(g.c.g)`
`=>BD=CE` ( 2 cạnh t/ứng )(đpcm)
13 tháng 3 2023
A B C D E
BD là đường phân giác của góc B nên ta có :
\(\widehat{ABD}=\widehat{CBD}=\dfrac{1}{2}\widehat{B}\) ( 1 )
CE là đường phân giác của góc C nên ta có :
\(\widehat{ACE}=\widehat{BCE}=\dfrac{1}{2}\widehat{C}\) ( 2 )
Từ ( 1 ) , ( 2 ) = > \(\widehat{ABD}=\widehat{ACE}\)
Xét tam giác ADB và tam giác AEC ta có :
Góc A chung
AB = AC ( gt )
\(\widehat{ABD}=\widehat{ACE}\) ( cmt )
= > \(\Delta ABD=\Delta ACE\left(g-c-g\right)\)
= > BD = CE ( 2 cạnh tương ứng )