Tìm m để \(x^3+mx-6\) chia hết cho \(x^2-2x-3\)
(bằng cách dùng sơ đồ Hoocne nhé)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 10 2016
Tìm m để
a, (x^4+5x^3-x^2-17x+m+4)chia hết cho (x^2+2x-3)
b, (2x^4+mx^3-mx-2) chia hết cho (x^2-1)
KN
13 tháng 12 2019
x^2-2x+3 2x^3-9x^2+mx-15 2x-5 2x^3-4x^2+6x -5x^2+(m-6)x-15 -5x^2+10x-15 (m-16)x
Để đa thức 2x3-9x2+mx-15 chia hết cho đa thức x2-2x+3 thì \(\left(m-16\right)x=0\Rightarrow m-16=0\Rightarrow m=16\)
Vậy m = 16 thì đa thức 2x3-9x2+mx-15 chia hết cho đa thức x2-2x+3
13 tháng 12 2019
2x^3-9x^2+mx-15 x^2-2x+3 2x+13 2x^3-4x^2+6x 13x^2+x(m-6)-15 13x^2-26x +39 x(m+20)-54
Đến đây làm sao nữa ta ?
VB
0
5 tháng 12 2023
a: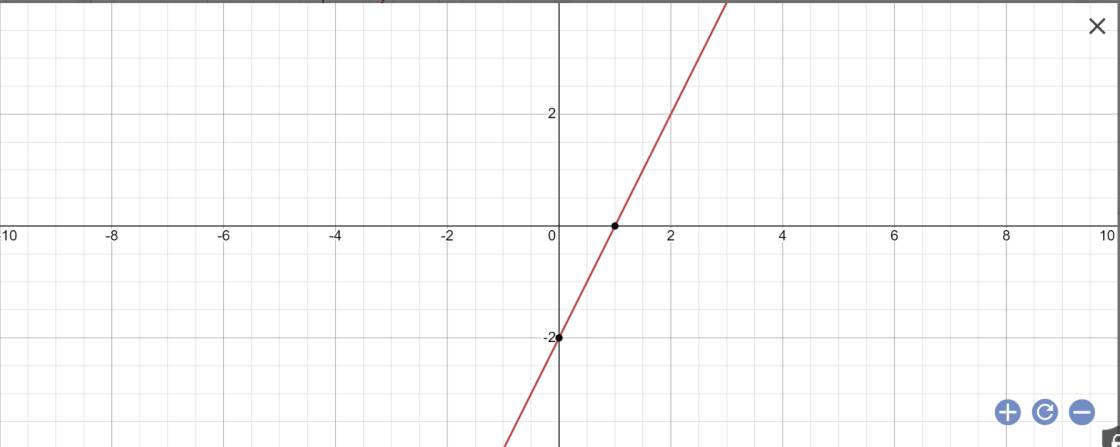 
b: Để (d)//(d') thì \(\left\{{}\begin{matrix}m+1=2\\6< >-2\left(đúng\right)\end{matrix}\right.\)
=>m+1=2
=>m=1
c:
(d'): y=(m+1)x+6
=>(m+1)x-y+6=0
Khoảng cách từ O đến (d') là:
\(d\left(O;\left(d'\right)\right)=\dfrac{\left|0\cdot\left(m+1\right)+0\cdot\left(-1\right)+6\right|}{\sqrt{\left(m+1\right)^2+\left(-1\right)^2}}\)
\(=\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}\)
Để \(d\left(O;\left(d'\right)\right)=3\sqrt{2}\) thì \(\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}=3\sqrt{2}\)
=>\(\sqrt{\left(m+1\right)^2+1}=\sqrt{2}\)
=>\(\left(m+1\right)^2+1=2\)
=>\(\left(m+1\right)^2=1\)
=>\(\left[{}\begin{matrix}m+1=1\\m+1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-2\end{matrix}\right.\)
HN
25 tháng 12 2018
Với tất cả các câu, mk chỉ làm ngắn gọn. Nếu bn muốn đầy đủ, thì bn tự lập bảng rồi xét.
1. \(13⋮\left(x-3\right)\)
\(\Leftrightarrow\left(x-3\right)\inƯ\left(13\right)=\left\{\pm1;\pm13\right\}\)
\(\Rightarrow x\in\left\{2;4;-10;16\right\}\)
Vậy x = ......................
2. \(\left(x+13\right)⋮\left(x-4\right)\)
\(\Leftrightarrow\left(x-4\right)+17⋮\left(x-4\right)\)
\(\Leftrightarrow17⋮x-4\)
\(\Leftrightarrow\left(x-4\right)\inƯ\left(17\right)=\left\{\pm1;\pm17\right\}\)
\(\Rightarrow x\in\left\{3;5;-13;21\right\}\)
Vậy x = ...................
3. \(\left(2x+108\right)⋮\left(2x+3\right)\)
\(\Leftrightarrow\left(2x+3\right)+105⋮\left(2x+3\right)\)
\(\Leftrightarrow105⋮\left(2x+3\right)\)
\(\Leftrightarrow\left(2x+3\right)\inƯ\left(105\right)\)\(=\left\{\pm1;\pm3;\pm5;\pm7;\pm15;\pm21;\pm35;\pm105\right\}\)
\(\Rightarrow x=-2;-1;-3;0;-4;1;-5;2;...............\)
4. \(17x⋮15\)
\(\Leftrightarrow x⋮15\) ( vì \(\left(15,17\right)=1\) )
Do đó : Với mọi x thuộc Z thì \(17x⋮15\)
HN
25 tháng 12 2018
6. \(\left(x+16\right)⋮\left(x+1\right)\)
\(\Leftrightarrow\left(x+1\right)+15⋮\left(x+1\right)\)
\(\Leftrightarrow15⋮\left(x+1\right)\)
\(\Leftrightarrow\left(x+1\right)\inƯ\left(15\right)=\left\{\pm1;\pm3;\pm5;\pm15\right\}\)
\(\Rightarrow x\in\left\{-2;0;-4;2;-6;4;-16;14\right\}\)
Vậy x = .....................
7. \(x⋮\left(2x-1\right)\)
Mà \(\left(2x-1\right)\) lẻ
Nên : Với mọi x thuộc Z là số lẻ thì \(x⋮\left(2x-1\right)\)
8. \(\left(2x+3\right)⋮\left(x+5\right)\)
\(\Leftrightarrow\left(2x+10\right)-7⋮\left(x+5\right)\)
\(\Leftrightarrow2.\left(x+5\right)-7⋮\left(x+5\right)\)
\(\Leftrightarrow7⋮\left(x+5\right)\)
\(\Leftrightarrow\left(x+5\right)\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\)
\(\Rightarrow x\in\left\{-6;-4;-12;2\right\}\)
Vậy x = .........................