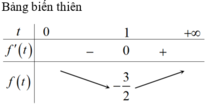
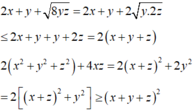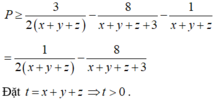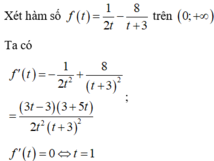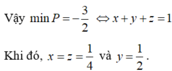Cho ba số dương x; y; z. CMR: \(x^2\left(x-\sqrt{yz}\right)+y^2\left(y-\sqrt{xz}\right)+z^2\left(z-\sqrt{xy}\right)\ge0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Em chung họ nguyển với anh em xin được làm quen với anh NGUYỄN THÀNH NAM

- Nếu \(x=0\Rightarrow yz=0\Rightarrow\left[{}\begin{matrix}y=0\\z=0\end{matrix}\right.\) \(\Rightarrow\) có ít nhất 2 số bằng 0 trái giả thiết chỉ một số bằng 0 \(\Rightarrow x\ne0\)
- Nếu \(y=0\Rightarrow x^3=0\Rightarrow x=0\Rightarrow x=y=0\) trái giả thiết giống bên trên \(\Rightarrow y\ne0\)
\(\Rightarrow z=0\)
\(\Rightarrow x^3=-xy\Rightarrow x^2=-y\Rightarrow y=-x^2< 0\)
Vậy \(\left\{{}\begin{matrix}x>0\\y< 0\\z=0\end{matrix}\right.\)

giả sử x =0 khi đó y(z-0)=0 nên y=0 hoặc z=0 (trái vs giả thiết )
Giả sử y=0 khi đó x3=0 ( trái với giả thiết )
Vậy z=0
Khi z=0 ta có x3=y(-x)
<=> x2=-y
vì x2 \(\ge0\)với mọi x suy ra y\(\le\)0 nên y là số âm
vậy còn lại x là số dương

Bạn vô tham khảo nha Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học toán với OnlineMath
http://olm.vn/hoi-dap/question/224185.html
Bạn vào đây tham khảo nha !!!
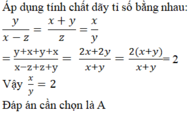
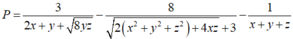 đạt giá trị nhỏ nhất. Tính
.
đạt giá trị nhỏ nhất. Tính
.