Mọi người giúp mình với ạ :'( .Viết đoạn văn (khoảng 10 - 12 câu) theo mô hình diễn dịch nêu cảm nhận về tâm trạng người tù qua khổ thơ cuối bài "Khi con tu hú". Trong đoạn có sử dụng câu trần thuật
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{24\cdot12}{24+12}=8\Omega\)
\(I=\dfrac{U}{R}=\dfrac{12}{8}=1,5A\)
\(P=\dfrac{U^2}{R}=\dfrac{12^2}{8}=18W\)
\(Q_{tỏa1}=A_1=U_1\cdot I_1\cdot t=12\cdot\dfrac{12}{24}\cdot1\cdot3600=21600J\)
\(Q_{tỏa2}=A_2=U_2\cdot I_2\cdot t=12\cdot\dfrac{12}{12}\cdot1\cdot3600=43200J\)

Bài 3.
Định luật ll Niu-tơn:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}=m\cdot\overrightarrow{a}\)
\(\Rightarrow F-F_{ms}=m\cdot a\)
Gia tốc vật:
\(a=\dfrac{F-F_{ms}}{m}=\dfrac{4,5-\mu mg}{m}=\dfrac{4,5-0,2\cdot1,5\cdot10}{1,5}=1\)m/s2
Vận tốc vật sau 2s:
\(v=a\cdot t=1\cdot2=2\)m/s

Bài 3:
a, Lực hấp dẫn giữa Trái Đất và Mặt Trăng
\(F_{hd}=G\cdot\dfrac{M_1M_2}{r^2}=6,67\cdot10^{-11}\cdot\dfrac{6\cdot10^{24}\cdot7,2\cdot10^{22}}{\left(3,84\cdot10^8\right)^2}=1,95\cdot10^{20}\left(N\right)\)

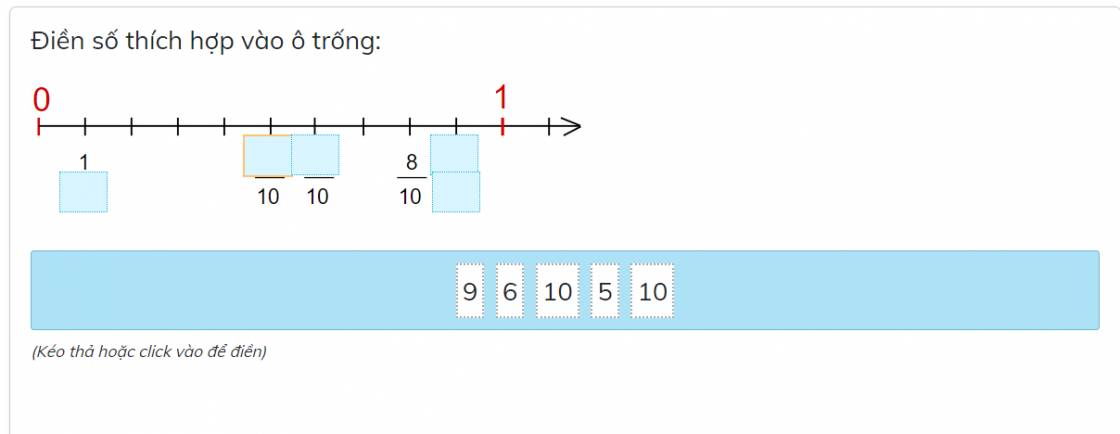
Từ 0 đến 1 được chia thành 10 phần bằng nhau.
Giá trị của mỗi phần là: \(\dfrac{1}{10}\)
Từ lập luận trên ta có:
Số thích hợp để điền vào các ô trống lần lượt là:
10; 5; 6; 9; 10
0 ; 1/10 ; 2/10 ; 3/10 ; 4/10 ; 5/10 ; 6/10 ; 7/10 ; 8/10 ; 9/10 ; 1
Chúc bạn học tốt!





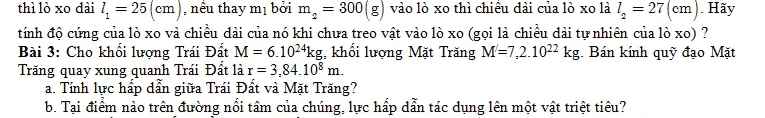
 Mọi người giải giúp mình với ạ mình đang cần gấp ạ, giúp mình nhé
Mọi người giải giúp mình với ạ mình đang cần gấp ạ, giúp mình nhé 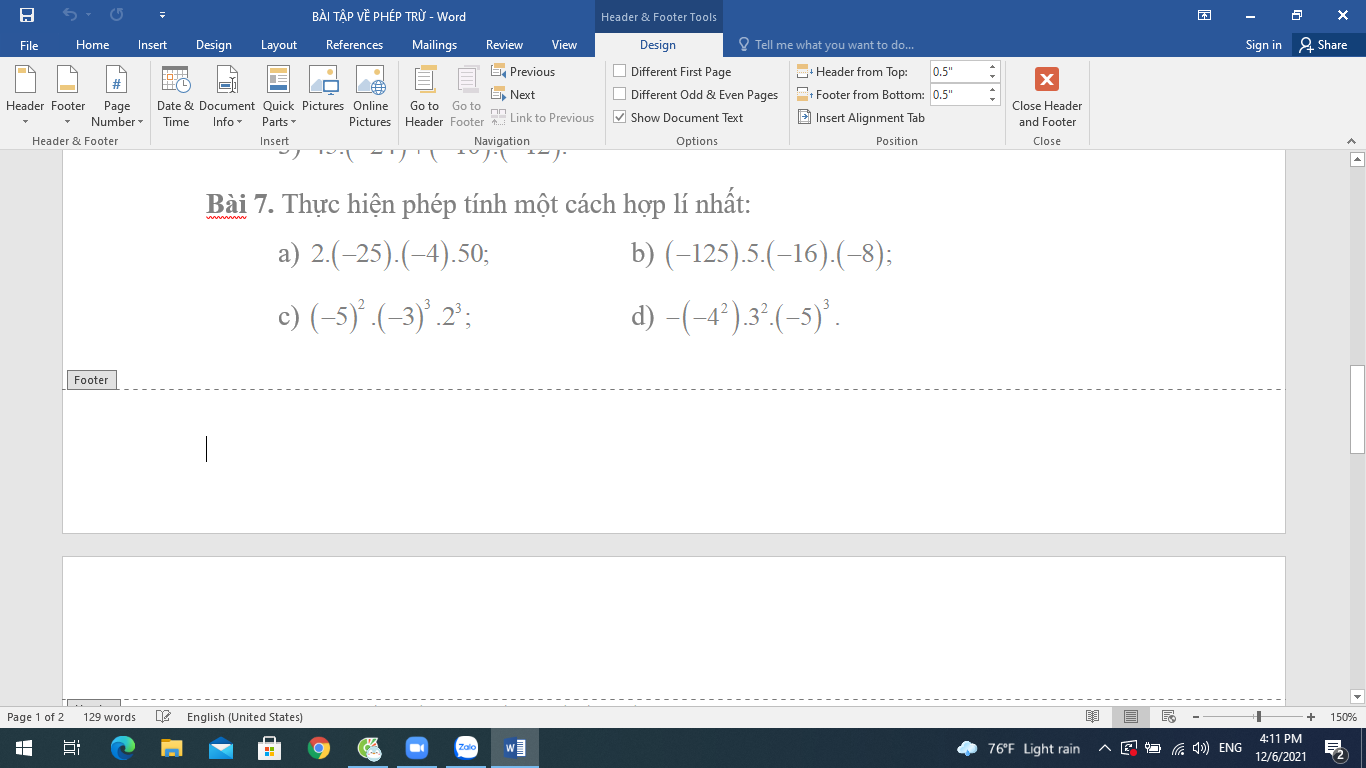
tham khảo
Ta nghe hè dậy bên lòng
Mà chân muốn đạp tan phòng, hè ôi!
Ngột làm sao, chết uất thôi
Con chim tu hú ngoài trời cứ kêu!
Tưởng như sự liên kết giữa hai đoạn thơ này không thật chặt chẽ và tứ thơ không liên tục. Khi hướng ra bên ngoài, nhà thơ tả cảnh nhưng khi hướng vào trong lại tả tâm trạng. Kì thực đây chính là sự liên kết vô cùng khéo léo và tinh tế. Mối dây liên kết ấy chính là tiếng chim tu hú. Tiếng chim gọi bầy tha thiết gợi mở một thế giơi bao la và vô cùng sinh động. Nhưng thế giới đó càng rộng rãi, rực rỡ bao nhiêu thì lại càng khiến cho người tù (đã bị tách biệt khỏi thế giới ấy) cảm thấy ngột ngạt và khao khát bấy nhiêu.Tiếng chim tu hú ở đầu và cuối của bài thơ tuy đều biểu trưng cho tiếng gọi tha thiết của tự do, của cuộc sống ngoài kia đầy quyến rũ đối với người tù nhưng tâm trạng của người tù khi nghe tiếng tu hú lại rất khác nhau, ở câu thơ đầu, tiếng tu hú gợi hình ảnh cuộc sống đầy hương sắc, từ đó gợi ra cái khát khao về cuộc sống tự do. Thế nhưng, đến câu kết, tiếng chim ấy lại khiến cho người tù cố cảm giác bực bội, đau khổ vì chưa thể thoát ra khỏi cảnh tù dầy.
Mình cảm ơn bạn