Tìm a,b,c biết: (ax+b).(x2+cx+1)=x3-3x+2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 6 2016
a) ax^2 + bx + c = 0
Để phương trình thỏa mãn điều kiện có 2 nghiệm dương phân biệt.
∆ > 0
=> b^2 - 4ac > 0
x1 + x2 = -b/a > 0
=> b và a trái dấu
x1.x2 = c/a > 0
=> c và a cùng dấu
Từ đó ta xét phương trình cx^2 + bx^2 + a = 0
∆ = b^2 - 4ac >0
x3 + x4 = -b/c, vì a và c cùng dấu mà b và a trái dấu nên b và c trái dấu , vì vậy -b/c >0
x3.x4 = a/c, vì a và c cùng dấu nên a/c > 0
=> phương trình cx^2 + cx + a có 2 nghiệm dương phân biệt x3 và x4
Vậy nếu phương trình ax^2 + bx + c = 0 có 2 nghiệm dương phân biệt thì phương trình cx^2 + bx + a = 0 cũng có 2 nghiệm dương phân biệt.
b) Ta có, vì x1, x2, x3, x4 không âm, dùng cô si.
x1 + x2 ≥ 2√( x1.x2 )
x3 + x4 ≥ 2√( x3x4 )
=> x1 + x2 + x3 + x4 ≥ 2[ √( x1.x2 ) + √( x3x4 ) ] (#)
Tiếp tục côsi cho 2 số không âm ta có
√( x1.x2 ) + √( x3x4 ) ≥ 2√[√( x1.x2 )( x3.x4 ) ] (##)
Theo a ta có
x1.x2 = c/a
x3.x4 = a/c
=> ( x1.x2 )( x3.x4 ) = 1
=> 2√[√( x1.x2 )( x3.x4 ) ] = 2
Từ (#) và (##) ta có
x1 + x2 + x3 + x4 ≥ 4
19 tháng 12 2021
a: \(\Leftrightarrow x\left(x-5\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\\x=-5\end{matrix}\right.\)
30 tháng 9 2021
\(A=6x^2+23x+21-\left(6x^2+23x-55\right)=76\\ B=x^4+x^3-x^2-2x^2-2x+2-x^4-x^3+3x^2+2x\\ =2\\ C=x^4+x^3-3x^2-2x-\left(x^4+x^3-x^2-2x^2-2x+2\right)\\ =-2\)
1 tháng 11 2021
a) \(\Rightarrow x\left(x+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=-3\end{matrix}\right.\)
b) \(\Rightarrow x\left(x^2-4\right)=0\Rightarrow x\left(x-2\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
c) \(\Rightarrow\left(x-1\right)\left(5x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{5}\end{matrix}\right.\)
d) \(\Rightarrow2\left(x+5\right)-x\left(x+5\right)=0\Rightarrow\left(x+5\right)\left(2-x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-5\\x=2\end{matrix}\right.\)
e) \(\Rightarrow2x^2-10x-3x-2x^2=26\)
\(\Rightarrow-13x=26\Rightarrow x=-2\)
f) \(\Rightarrow\left(x-2012\right)\left(5x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2012\\x=\dfrac{1}{5}\end{matrix}\right.\)
CM
16 tháng 12 2018
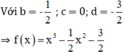
a) f’(x) = 3x2 – x.
⇒ f’(-1) = 4; f(-1) = -3.
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = -1 là:
y = 4.(x + 1) – 3 = 4x + 1.
b) f’(sin x) = 0
⇔ 3.sin2x – sin x = 0
⇔ sin x.(3sin x – 1) = 0
CM
11 tháng 9 2019
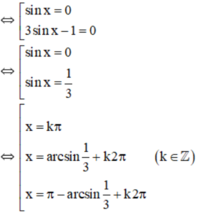
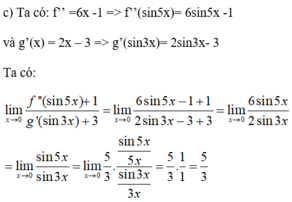
a) x = 1; x = - 1 3 b) x = 2.
c) x = 3; x = -2. d) x = -3; x = 0; x = 2.
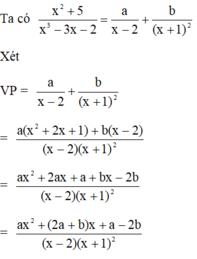
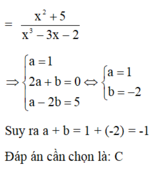
a) S hình thoi là:
(19 x 12) : 2 = 114(cm2)
b) S hình thoi là;
(30 x 7) : 2 = 105(cm2)
(ax+b).(x2+cx+1)=x3-3x+2
ax3+acx2+ax+bx2+cbx+b=x3-3x+2
ax3+(acx2+bx2)+(ax+cbx)+b=x3-3x+2
ax3+x2(ac+b)+x(a+cb)+b=x3+0x2-3x+2
Đồng nhất các hệ số 2 vế của đẳng thức,ta có:
\(\hept{\begin{cases}a=1,b=2\\ac+b=0\\a+cb=-3\end{cases}}\Rightarrow\hept{\begin{cases}a=1,b=2\\c=-2\end{cases}}\)
Vậy a=1,b=2,c=-2 thì thỏa mãn đẳng thức đã cho
P/s:cái ngoặc nhọn của OLM chỉ điền đc 3 ô thui nhưng trình bày vào vở thì trình bày cái ngoặc nhọn cho 4 dòng nhé :))