Phân tích đa thức thành nhân tử:
(6p+1)^2-12(6p+1)+36
81-18(7k-5)+(5-7k)^2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 9 2021
\(1,\\ 1,=15\left(x+y\right)\\ 2,=4\left(2x-3y\right)\\ 3,=x\left(y-1\right)\\ 4,=2x\left(2x-3\right)\\ 2,\\ 1,=\left(x+y\right)\left(2-5a\right)\\ 2,=\left(x-5\right)\left(a^2-3\right)\\ 3,=\left(a-b\right)\left(4x+6xy\right)=2x\left(2+3y\right)\left(a-b\right)\\ 4,=\left(x-1\right)\left(3x+5\right)\\ 3,\\ A=13\left(87+12+1\right)=13\cdot100=1300\\ B=\left(x-3\right)\left(2x+y\right)=\left(13-3\right)\left(26+4\right)=10\cdot30=300\\ 4,\\ 1,\Rightarrow\left(x-5\right)\left(x-2\right)=0\Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\\ 2,\Rightarrow\left(x-7\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=7\\x=-2\end{matrix}\right.\\ 3,\Rightarrow\left(3x-1\right)\left(x-4\right)=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=4\end{matrix}\right.\\ 4,\Rightarrow\left(2x+3\right)\left(2x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=\dfrac{1}{2}\end{matrix}\right.\)
17 tháng 12 2017
Các nguyên tử này thuộc 2 nguyên tố hóa học.
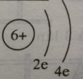
Nguyên tử (1), (3) thuộc cùng 1 nguyên tố do cùng có 6p
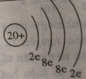
Nguyên tử (2), (4), (5) thuộc cùng 1 nguyên tố do cùng có 20p.
30 tháng 8 2019
Hai nguyên tố đó là: cacbon và canxi.
| Tên nguyên tố | Cacbon | Canxi |
|---|---|---|
| Kí hiệu | C | Ca |
| Nguyên tử khối | 12 | 40 |
MN
20 tháng 6 2021
(1) Hạt nhân có : 6 proton , 6 notron.
(2) Hạt nhân có : 20 proton , 20 notron.
(3) Hạt nhân có : 6 proton , 7 notron.
(4) Hạt nhân có : 20 proton , 22 notron.
(5) Hạt nhân có : 20 proton , 23 notron.
21 tháng 8 2021
a) 5 nguyên tử này thuộc 2 nguyên tố hóa học:
b) - Nguyên tố Cacbon (C): Nguyên tử (1),nguyên tử (3)
NTK(C)=12 (đ.v.C)
NTK(1)= 6+6=12(đ.v.C); NTK(3)= 6+7=13(đ.v.C)
- Nguyên tố Canxi (Ca): Nguyên tử (2), nguyên tử (4) và nguyên tử (5)
NTK(Ca)=40(đ.v.C)
NTK(2)=20+20=40(đ.v.C); NTK(4)=20+22=42(đ.v.C); NTK(5)= 20+23=43(đ.v.C)
U
0
24 tháng 10 2015
bài 1:= \(2x\left(x-3\right)-6\left(x-3\right)+2y\left(x-3\right)\)
=\(2\left(x-3\right)\left(x+y-3\right)\)
bài 2:P=\(x^2-2x+1+y^2+6y+9+2\)
P=\(\left(x-1\right)^2+\left(y+3\right)^2+2\ge2\)
vậy Pmin=2 khi x=1 và y=-3
a: \(=\left(6p+1-6\right)^2=\left(6p-5\right)^2\)
b: \(=\left(7k-5-9\right)^2=\left(7k-14\right)^2=49\cdot\left(k-2\right)^2\)
\(=\left(6p+1-6\right)^2=\left(6p-5\right)^2\)
\(=\left(9-5+7k\right)^2=\left(4+7k\right)^2\)