Mn ơi, hướng dẫn em cách để giống mẫu đi ạ!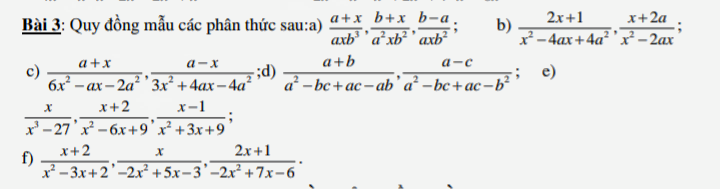
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
T
1
Những câu hỏi liên quan
T
0
10 tháng 9 2019
Viết các phân số dưới dạng tối giản:
0,3=310;−56;−123=−53;413;0;0,3=310;−56;−123=−53;413;0;−0,875=−8751000=−78−0,875=−8751000=−78
- So sánh các số hữu tỉ dương với nhau:
Ta có : 310=39130;413=40130310=39130;413=40130
Vì 39<4039<40 nên 310<413310<413
- Tương tự So sánh các số hữu tỉ âm với nhau ta được:
−56=−2024;−53=−4024;−78=−2124⇒−4024<−2124<−2024(Do−40<−21<−20)⇒−53<−78<−56−56=−2024;−53=−4024;−78=−2124⇒−4024<−2124<−2024(Do−40<−21<−20)⇒−53<−78<−56
Vậy:
TK
1
MH
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 8 2023
Phương trình bậc hai có dạng: a\(x^2\) + b\(x\) + c
Bước 1: Đưa nó về bình phương của một tổng hoặc một hiệu cộng với một số nào đó. nếu a > 0 thì em sẽ tìm giá trị nhỏ nhất; nếu a < 0 thì em sẽ tìm giá trị lớn nhất
Bước 2: lập luận chỉ ra giá trị lớn nhất hoặc nhỏ nhất
Bước 3: kết luận
Giải:
A = 3\(x^2\) - 5\(x\) + 3 Vì a = 3 > 0 vậy biểu thức A chỉ tồn tại giá trị nhỏ nhất
A = 3\(x^2\) - 5\(x\) + 3
A = 3.(\(x\)2 - 2.\(x\).\(\dfrac{5}{6}\) + \(\dfrac{25}{36}\)) + \(\dfrac{11}{12}\)
A = 3.(\(x\) - \(\dfrac{5}{6}\))2 + \(\dfrac{11}{12}\)
Vì (\(x-\dfrac{5}{6}\))2 ≥ 0 ⇒ 3.(\(x\) - \(\dfrac{5}{6}\))2 ≥ 0 ⇒ 3.(\(x-\dfrac{5}{6}\))2 + \(\dfrac{11}{12}\) ≥ \(\dfrac{11}{12}\)
Amin = \(\dfrac{11}{12}\) ⇔ \(x\) = \(\dfrac{5}{6}\)
Hướng dẫn em cách làm phần b với ạ :
12 tháng 12 2021
Câu c mình làm rồi: Mn ơi, hướng dẫn em cách để giống mẫu đi ạ! - Hoc24
\(d,\dfrac{x}{x^3-27}=\dfrac{x}{\left(x-3\right)\left(x^2+3x+9\right)}=\dfrac{x\left(x-3\right)}{\left(x-3\right)^2\left(x^2+3x+9\right)}\\ \dfrac{x+2}{x^2-6x+9}=\dfrac{x+2}{\left(x-3\right)^2}=\dfrac{\left(x+2\right)\left(x^2+3x+9\right)}{\left(x-3\right)^2\left(x^2+3x+9\right)}\\ \dfrac{x-1}{x^2+3x+9}=\dfrac{\left(x-1\right)\left(x-3\right)^2}{\left(x-3\right)^2\left(x^2+3x+9\right)}\)
\(f,\dfrac{x+2}{x^2-3x+2}=\dfrac{x+2}{\left(x-1\right)\left(x-2\right)}=\dfrac{\left(x+2\right)\left(2x-3\right)}{\left(x-1\right)\left(x-2\right)\left(2x-3\right)}\\ \dfrac{x}{-2x^2+5x-3}=\dfrac{-x}{\left(2x-3\right)\left(x-1\right)}=\dfrac{-x\left(x-2\right)}{\left(2x-3\right)\left(x-1\right)\left(x-2\right)}\\ \dfrac{2x+1}{-2x^2+7x-6}=\dfrac{-\left(2x+1\right)}{\left(x-2\right)\left(2x-3\right)}=\dfrac{-\left(2x+1\right)\left(x-1\right)}{\left(x-1\right)\left(x-2\right)\left(2x-3\right)}\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2021
\(\dfrac{a+x}{6x^2-ax-2a^2}=\dfrac{\left(a+x\right)}{\left(2x+a\right)\left(3x-2a\right)}\)
\(\dfrac{a-x}{3x^2+4ax-4a^2}=\dfrac{a-x}{\left(x+2a\right)\left(3x-2a\right)}\)
Do đó ta quy đồng:
\(\dfrac{a+x}{6x^2-ax-2a^2}=\dfrac{\left(a+x\right)\left(x+2a\right)}{\left(x+2a\right)\left(2x+a\right)\left(3x-2a\right)}\)
\(\dfrac{a-x}{3x^2+4ax-4a^2}=\dfrac{\left(a-x\right)\left(2x+a\right)}{\left(x+2a\right)\left(2x+a\right)\left(3x-2a\right)}\)
\(a,\dfrac{a+x}{axb^3}=\dfrac{a\left(a+x\right)}{a^2xb^3};\dfrac{b+x}{a^2xb^2}=\dfrac{b\left(b+x\right)}{a^2xb^3};\dfrac{b-a}{axb^2}=\dfrac{ab\left(b-a\right)}{a^2xb^3}\\ b,\dfrac{2x+1}{x^2-4ax+4a^2}=\dfrac{x\left(2x+1\right)}{x\left(x-2a\right)^2};\dfrac{x+2a}{x^2-2ax}=\dfrac{\left(x+2a\right)\left(x-2a\right)}{x\left(x-2a\right)^2}\\ c,\dfrac{a+x}{6x^2-ax-2a^2}=\dfrac{a+x}{\left(3x-2a\right)\left(2x+a\right)}=\dfrac{\left(a+x\right)\left(x+2a\right)}{\left(3x-2a\right)\left(2x+a\right)}\\ \dfrac{a-x}{3x^2+4ax-4a^2}=\dfrac{a-x}{\left(3x-2a\right)\left(x+2a\right)}=\dfrac{\left(a-x\right)\left(2x+a\right)}{\left(3x-2a\right)\left(x+2a\right)\left(2x+a\right)}\)