tìm giá trị nhỏ nhất của y=(2x3 -2x2 +1)/x2 với x>0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 12 2019
Hàm số có giá trị nhỏ nhất ⇔ y nhỏ nhất.
Dựa vào đồ thị nhận thấy cả ba hàm số đạt y nhỏ nhất tại điểm O(0; 0).
Vậy ba hàm số trên đều đạt giá trị nhỏ nhất tại x = 0.
22 tháng 6 2018
với x;y>=0 ta có:
\(A^2=\left(\sqrt{2x+1}+\sqrt{2y+1}\right)^2=2x+1+2y+1+2\sqrt{\left(2x+1\right)\left(2y+1\right)}\)
\(=2\left(x+y\right)+2+\sqrt{4xy+2x+2y+1}=2\left(x+y\right)+2+\sqrt{4xy+2\left(x+y\right)+1}\)
\(2=2\left(x^2+y^2\right)=\left(1+1\right)\left(x^2+y^2\right)>=\left(x+y\right)^2\Rightarrow x+y< =\sqrt{2}\)(bđt bunhiacopxki)
\(2xy< =x^2+y^2=1\Rightarrow2\cdot2xy=4xy< =2\cdot1=2\)
\(\Rightarrow A^2=2\left(x+y\right)+2+2\sqrt{4xy+2\left(x+y\right)+1}< =2\sqrt{2}+2+2\sqrt{2+2\sqrt{2}+1}\)
\(=2\sqrt{2}+2+2\sqrt{\left(\sqrt{2}+1\right)^2}=2\sqrt{2}+2+2\left(\sqrt{2}+1\right)4\sqrt{2}+4\)
\(\Rightarrow A< =\sqrt{4\sqrt{2}+4}\)
dấu = xảy ra khi x=y=\(\sqrt{\frac{1}{2}}\)
vậy max A là \(\sqrt{4\sqrt{2}+4}\)khi \(x=y=\sqrt{\frac{1}{2}}\)
AH
Akai Haruma
Giáo viên
3 tháng 2 2024
Câu 1:
$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$
Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$
Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.
AH
Akai Haruma
Giáo viên
3 tháng 2 2024
Câu 2:
Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$
Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$
Với $x\in (1;3)$ thì hàm luôn nghịch biến
$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$
$\Rightarrow$ hàm không có min, max.
CM
21 tháng 10 2019
Phương trình 2 x 2 - 4 m x - 1 = 0 có ∆ ' = 4 m 2 + 2 > 0 nên phương trình có hai nghiệm phân biệt x 1 , x 2 với S = x 1 + x 2 = 2 m , P = x 1 x 2 = - 1 2
Ta có: T 2 = x 1 - x 2 2 = S 2 - 4 P = 4 m 2 + 2 ≥ 2 ⇒ T ≥ 2
Dấu bằng xảy ra khi m = 0.
Vậy m i n T = 2
Đáp án cần chọn là: B
CM
10 tháng 4 2019
Ta có: x 3 + 2 x 2 - x - 2 = x 2 x + 2 - x + 2 = x 2 - 1 . x + 2 = x + 1 x - 1 x + 2
Do đó, để x 3 + 2 x 2 - x - 2 ≠ 0 khi (x + 2)(x – 1)(x + 1) ≠ 0 ⇒ x ≠ - 2 và x ≠ ± 1
Ta có: x = 1000001 thỏa mãn điều kiện.
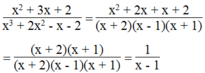
Thay x = 1000001 vào biểu thức ta được: 
17 tháng 12 2023
Bài 1:
a: \(M=x^2-10x+3\)
\(=x^2-10x+25-22\)
\(=\left(x^2-10x+25\right)-22\)
\(=\left(x-5\right)^2-22>=-22\forall x\)
Dấu '=' xảy ra khi x-5=0
=>x=5
b: \(N=x^2-x+2\)
\(=x^2-x+\dfrac{1}{4}+\dfrac{7}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>=\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi x-1/2=0
=>x=1/2
c: \(P=3x^2-12x\)
\(=3\left(x^2-4x\right)\)
\(=3\left(x^2-4x+4-4\right)\)
\(=3\left(x-2\right)^2-12>=-12\forall x\)
Dấu '=' xảy ra khi x-2=0
=>x=2
CM
16 tháng 2 2018
Ta có:
x 2 - x y + 3 = 0 1 2 x + 3 y - 14 ≤ 0 2
Do x,y>0 nên ⇔ x 2 + 3 x thay vào (2) ta được:
2 x + 3 . x 2 + 3 x - 14 ≤ 0
⇔ 2 x 2 + 3 x 2 + 9 - 14 x x ≤ 0
⇔ 5 x 2 - 14 x + 9 ≤ 0 ⇔ 1 ≤ x ≤ 9 5
Thay y = x 2 + 3 x vào P ta được:
P = 3 x 2 y - x y 2 - 2 x 3 + 2 x
= 3 x 2 . x 2 + 3 x - x . x 2 + 3 x 2 - 2 x 3 + 2 x
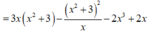
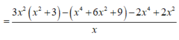
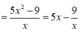
P ' = 5 + 9 x 2 > 0 với mọi x nên hàm số P=P(x) đồng biến trên 1 ; 9 5
Vậy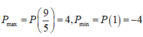 
Tổng 
.
Chọn đáp án B.
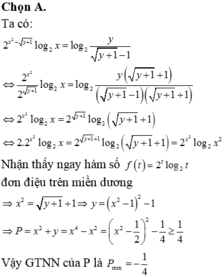
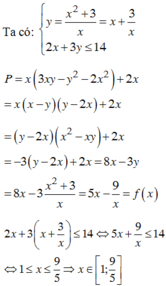
ta có
\(y=2x+\frac{1}{x^2}-2\)
hay \(y=x+x+\frac{1}{x^2}-2\ge3\sqrt[3]{\frac{x.x.1}{x^2}}-2=3-2=1\)
vậy giá trị nhỏ nhất của y là 1
Dấu bằng xảy ra khi \(x=\frac{1}{x^2}\Leftrightarrow x=1\)