Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có trực tâm O . Gọi M là trung điểm của BC; N,P lần lượt là chân đường cao kẻ từ B và C . Đường tròn đi qua 3 điểm M,N,P có phương trình : (T) : \(\left(x-1\right)^{^{ }2}+\left(y+\dfrac{1}{2}\right)^2=\dfrac{25}{4}\) . Phương trình đường tròn ngoại tiếp tam giác ABC là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 4 2018
Ta có A H → = a + 3 ; b ; B C → = − 1 ; 6 B H → = a − 3 ; b ; A C → = 5 ; 6 .
Từ giả thiết, ta có:
A H → . B C → = 0 B H → . A C → = 0 ⇔ a + 3 . − 1 + b .6 = 0 a − 3 .5 + b .6 = 0 ⇔ a = 2 b = 5 6 ⇒ a + 6 b = 7.
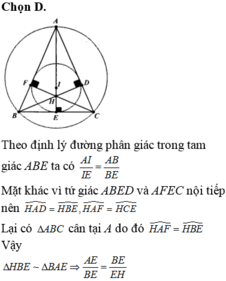
Chọn C.
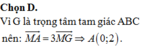
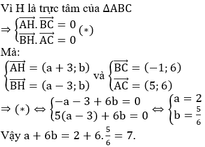
Đường tròn ngoại tiếp tam giác ABC là ảnh của đường tròn (T) qua phép vị tự tâm O tỉ số \(k=2\)
\(\Rightarrow\) Phương trình đường tròn ngoại tiếp tam giác:
\(\left(x-2\right)^2+\left(y+1\right)^2=25\)
(Tọa độ tâm nhân 2 lần và bán kính nhân 2 lần)