Cho đường tròn (O;R) chia đường tròn này thành ba cung có số đo tỉ lệ với 3,4,5.Tính diện tích các hình quạt tròn được tạo thành
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 12 2017
kẻ OH vuông góc với AB.
H là trung điểm của AB (theo tính chất bán kính và dây cung)
HA = HB = AB : 2 = 24: 2 = 12 (cm)
Và OH = 9 (gt)
Xét tam giác OHA vuông tại H
Theo pitago ta có: OA2 = OH2 + HB2 = 92 + 122 = 81 + 144 = 225
=> OA = 15 (cm) đây chính là bán kính của đường tròn
31 tháng 1 2023
a: Xét tứ giác AEHF có
góc AEH+góc AFH=180 độ
=>AEHF là tứ giác nội tiếp
Xét tứ giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC là tứ giác nội tiếp
b: Xét (O) có
ΔABK nội tiếp
AK là đường kính
=>ΔABK vuông tại B
=>BK//CH
Xét (O) có
ΔACK nội tiếp
AK là đường kính
=>ΔACK vuông tại C
=>CK//BH
Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
=>I là trung điểm của BC
Gọi x,y,z lần lượt là số đo độ của ba cung
ta có: x + y + z = 360 °
Theo đề bài ta có: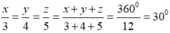
suy ra: x = 3. 30 ° = 90 ° ; y = 4. 30 ° = 120 ° ;z = 5. 30 ° = 150 °
Diện tích hình quạt tương ứng với các cung 90 ° , 120 ° , 150 ° là :