Cho hàm số y = f x = e a x − e 3 x 2 x khi x ≠ 0 1 2...

PT

Pham Trong Bach

22 tháng 1 2018

Cho hàm số y = f x = e a x − e 3 x 2 ...

Đọc tiếp

#Hỏi cộng đồng OLM #Mẫu giáo

1

CM

Cao Minh Tâm

22 tháng 1 2018

Đáp án là B

Đúng(0)

NP

Nhung Phan Hồng

12 tháng 1 2022

. a) Cho hàm số y = f(x) = -2x + 3. Tính f(-2) ;f(-1) ; f(0) ; f( 1 2  ); f( 1 2 ). b) Cho hàm số y = g(x) = x 2 – 1. Tính g(-1); g(0

giúp e với ạ

#Hỏi cộng đồng OLM #Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

12 tháng 1 2022

a: f(-2)=4+3=7

f(-1)=2+3=5

f(0)=3

f(1/2)=-1+3=2

f(-1/2)=1+3=4

b: g(-1)=1-1=0

f(0)=0-1=-1

Đúng(0)

VQ

Vương Quốc Anh

9 tháng 12 2015 - olm

Cho y=f(x)=2x-3.2

a) Tính f(x) khi x=1, x=10.

b) Tính x khi y=4, y=14

c) Những điểm nào sau đây không thuộc đồ thị hàm số f(x)?

A(3 ; 0) ; B($\frac{1}{2}$ ; -5) ; C(5; 2) ; D(0 ; -1) ; E(0; -6); F(12; 8)

#Hỏi cộng đồng OLM #Toán lớp 7

1

B

buitanquocdat

10 tháng 12 2015

a) Ta co: y = f(x) = 2x-3.2

Khi x=1 thi: f(x) = 2x - 3.2 = 2.1-3.2 = 2-6 = -4

Khi x=10 thi: f(x) = 2x-3.2 = 2.10-3.2 = 20-6 = 14

b) Tu y = 2x - 3.2 => x = (y+6):2

Khi y = 4 thi x=5

Khi y=14 thi x=10

c) Ta co: f(x) = 2x-3.2 = 2x-6

Xet A thay A co: y = 2x - 6 = 0 ( 0 = 0) => A thuoc do thi
Xet B thay B co: y = 2x-6 = -5 ( -5 = -5) => A thuoc do thi
Xet C thay C co: y=2x-6 = 4 ( 4 $\ne$ 2 ) => C khong thuoc do thi
Xét D thấy D có: y=2x-6 = -4 ( -4 khác -1 ) => D không thuộc đô thị
Xet E, E co: y =2x-6 = -6 ( -6 = -6 ) => S thuoc do thi
Xet F, F co: y = 2x-6 = 18 ( 18 khac 8) => F khong thuoc do thi

Vay: nhung diem khong thuoc do thi f(x) gom: C ; D ; F

Đúng(0)

LN

Linh Nguyễn

22 tháng 10 2021

cho hàm số y =f(x) =$\left\{{}\begin{matrix}\dfrac{2}{x-1}\\\sqrt{x+1}\\x^{2^{ }}-1\end{matrix}\right.$

khi x< 0 ; khi 0 ≤ x ≤ 2 ; khi x>2

a. Tìm tập xác định của hàm số.

b. Tính f(-1), f(0), f(1), f(2), f(3).

#Hỏi cộng đồng OLM #Toán lớp 10

1

NL

Nguyễn Lê Phước Thịnh

22 tháng 10 2021

a: TXĐ: D=R

b: $f\left(-1\right)=\dfrac{2}{-1-1}=\dfrac{2}{-2}=-1$

$f\left(0\right)=\sqrt{0+1}=1$

$f\left(1\right)=\sqrt{1+1}=\sqrt{2}$

$f\left(2\right)=\sqrt{3}$

Đúng(1)

S

SIeumvp9326

19 tháng 9 2021

cho hàm số y = ( 2 - căn 3 ) x - 1 . a . Hàm số y đồng biến hay nghịch biến trên R ? Vì sao ? . b . Tính f ( 2 + căn 3 ) , f ( căn 3) . c . Tính x khi y = căn 3 - 3 giúp e với ạ

#Hỏi cộng đồng OLM #Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

19 tháng 9 2021

a: Hàm số này đồng biến vì $2-\sqrt{3}>0$

b: $f\left(2+\sqrt{3}\right)=4-3-1=0$

$f\left(\sqrt{3}\right)=2\sqrt{3}-3-1=2\sqrt{3}-4$

Đúng(1)

DH

diệp hoàng

18 tháng 4 2023

( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$

#Hỏi cộng đồng OLM #Toán lớp 12

1

NL

Nguyễn Lê Phước Thịnh

19 tháng 4 2023

Chọn C

Đúng(0)

DH

diệp hoàng

19 tháng 4 2023

em muốn hỏi cách làm ấy ạ? hướng giải là như nào ấy ạ

Đúng(0)

PT

Pham Trong Bach

16 tháng 6 2019

Cho hàm số y=f(x) thỏa mãn f ' ( x ) + 2 x f ( x ) = e - x 2 , ∀ x ∈ R và f(1)=0 Tính giá trị f(2). ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 12

1

CM

Cao Minh Tâm

16 tháng 6 2019

Đáp án B.

Đúng(0)

TT

Thom tran thi

22 tháng 4 2016 - olm

Đạo hàm y 0 = −3x 2 + 6x + m − 1. Hàm số đã cho đồng biến trên khoảng (0; 3) khi và chỉ khi y 0 > 0, ∀x ∈ (0; 3). Hay −3x 2 + 6x + m − 1 > 0, ∀x ∈ (0; 3) ⇔ m > 3x 2 − 6x + 1, ∀x ∈ (0; 3) (∗). Xét hàm số f(x) = 3x 2 − 6x + 1 trên đoạn [0; 3] có f 0 (x) = 6x − 6; f 0 (x) = 0 ⇔ x = 1. Khi đó f(0) = 1, f(3) = 10, f(1) = −2, suy ra max [0;3] f(x) = f(3) = 10. Do đó (∗) ⇔ m > max [0;3] f(x) ⇔ m > 10. Vậy với m > 10 thì hàm số...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 9

1

TT

Thom tran thi

22 tháng 4 2016

ai làm có thưởng 2điem

Đúng(0)

PT

Pham Trong Bach

20 tháng 2 2019

Cho hàm số y= f( x) = ax4+ bx3+ cx2+ dx+ e với a ≠0. Biết rằng hàm số y= f( x) có đạo hàm là f’(x) và hàm số y= f’(x) có đồ thị như hình vẽ bên. Khi đó nhận xét nào sau đây là sai? A. Trên khoảng (-2; 1) thì hàm số y= f( x) luôn tăng. B. Hàm số y= f(x) giảm trên đoạn [ -1; 1] . C. Hàm số y= f( x) đồng biến trên khoảng (1+ ∞) . D. Hàm số y= f( x) nghịch biến trên khoảng (- ∞; -2)...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 12

1

CM

Cao Minh Tâm

20 tháng 2 2019

Chọn C

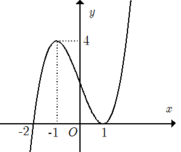
Trên đoạn [ - 1; 1] đồ thị hàm số y= f’( x) nằm phía trên trục hoành.

=> Trên đoạn [ - 1; 1] thì f’( x) > 0.

=> Trên đoạn [ - 1; 1] thì hàm số y= f( x) đồng biến

Đúng(0)

BB

Bé Bảo

2 tháng 12 2015 - olm

Vẽ đồ thị hàm số y=f(x)=-0.5x

a f(2);f(-2);f(4);f(0)

b giá trị của x khi y=-1 y=0 y=2.5

c các giá trị của x khi dương, khi âm

các ac giải giúp e phần bc thôi ạ còn phần a e làm dc r` ạ

#Hỏi cộng đồng OLM #Toán lớp 7

1

ND

Nguyễn Đặng Quốc Huy

2 tháng 12 2015

thế y = -1 vào hàm số y= f(x) = -0.5x ta được :

-1 = - 0.5x

=>x =(-1) : (-0.5)

=>x = 2

Làm tương tự nhé

Đúng(0)

AD

anh dat

2 tháng 1 2022

Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Với các hàm số bậc nhất, hãy cho biết hàm số đó đồng biến hay nghịch biến? a)y=5-2x b)y=x√2-1. C)y=2(x+1)-2x. D)y=3(x-1)x. e)y=-2/3 x. f)y=x+ 1/x

#Hỏi cộng đồng OLM #Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

2 tháng 1 2022

Các hàm số a,b,e là các hàm số bậc nhất

Đúng(1)

AD

anh dat

2 tháng 1 2022

Giải thích chưa

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP