Cho số phức z thỏa mãn GTNN của biểu thức bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B.
Phương pháp:
Tọa độ hóa điểm số phức z, đánh giá GTNN.
Cách giải:
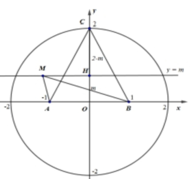
Giả sử z = x + y i , x , y ∈ R ⇒ M x ; y
là điểm biểu diễn của z trên mặt phẳng tọa độ Oxy.
P = 2 z + 1 + 2 z − 1 + z − z ¯ − 4 i
= 2 x + 1 2 + y 2 + x − 1 2 + y 2 + y − 2
Đặt A − 1 ; 0 , B 1 ; 0 , C 0 ; 2 và H 0 ; y là hình chiếu của M lên Oy. Khi đó, P = 2 M A + M B + M C
Ta xác định vị trí của M để P đạt giá trị nhỏ nhất, (M di chuyển trên hình tròn x 2 + y 2 ≤ 4 )
+) Nếu M ∈ C 1 : x 2 + y 2 ≤ 4 , y < 0 thì ta luôn tìm được điểm
M ' ∈ C 1 : x 2 + y 2 ≤ 4 , y ≥ 0 đối xứng với M qua Ox. Khi đó,
P = 2 M A + M B + H C
= 2 M ' A + M ' B + H ' C > 2 M A + M B + H C
+) Ta xét điểm
M ∈ C 2 : x 2 + y 2 ≤ 4 , y ≥ 0
Với M nằm trong nửa hình tròn C 2 , thay đổi trên đường thẳng y = m cố định 0 ≤ m ≤ 2 thì độ dài đoạn HC không đổi, M A + M B ≥ 2 2 H A + H C
Ta có:
2 H A + H C = 2 m 2 + 1 + 2 − m = f m , m ∈ 0 ; 2
f ' m = 2 m 2 + 1 − 1 , f ' m = 0 ⇔ m = 1 3
f m min = f 1 3 = 1 + 3 2
⇒ P min = 2 1 + 3 2 = 2 + 3
khi M 0 ; 1 3 hay z = i 3 .
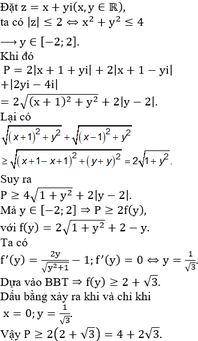

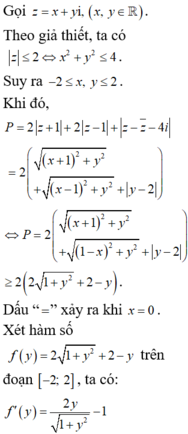
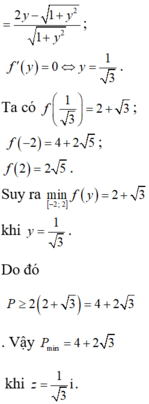

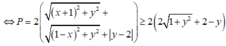
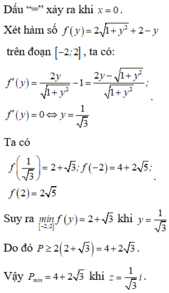
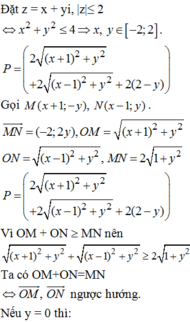
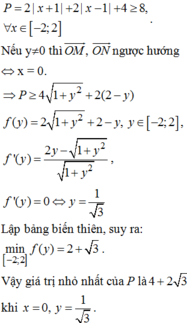


Đáp án B.
Phương pháp:
Tọa độ hóa điểm số phức z, đánh giá GTNN.
Cách giải:
Giả sử z = x + y i , x , y ∈ R ⇒ M x ; y
là điểm biểu diễn của z trên mặt phẳng tọa độ Oxy.
P = 2 z + 1 + 2 z − 1 + z − z ¯ − 4 i
= 2 x + 1 2 + y 2 + x − 1 2 + y 2 + y − 2
Đặt A − 1 ; 0 , B 1 ; 0 , C 0 ; 2 và H 0 ; y là hình chiếu của M lên Oy. Khi đó, P = 2 M A + M B + M C
Ta xác định vị trí của M để P đạt giá trị nhỏ nhất, (M di chuyển trên hình tròn x 2 + y 2 ≤ 4 )
+) Nếu M ∈ C 1 : x 2 + y 2 ≤ 4 , y < 0 thì ta luôn tìm được điểm
M ' ∈ C 1 : x 2 + y 2 ≤ 4 , y ≥ 0 đối xứng với M qua Ox. Khi đó,
P = 2 M A + M B + H C
= 2 M ' A + M ' B + H ' C > 2 M A + M B + H C
+) Ta xét điểm
M ∈ C 2 : x 2 + y 2 ≤ 4 , y ≥ 0
Với M nằm trong nửa hình tròn C 2 , thay đổi trên đường thẳng y = m cố định 0 ≤ m ≤ 2 thì độ dài đoạn HC không đổi, M A + M B ≥ 2 2 H A + H C
Ta có:
2 H A + H C = 2 m 2 + 1 + 2 − m = f m , m ∈ 0 ; 2
f ' m = 2 m 2 + 1 − 1 , f ' m = 0 ⇔ m = 1 3
f m min = f 1 3 = 1 + 3 2
⇒ P min = 2 1 + 3 2 = 2 + 3
khi M 0 ; 1 3 hay z = i 3 .