Cho Viết biểu thức về dạng và biểu thức về dạng Ta có
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho x > 0 , y > 0 và \(x+y\ge6\). Tìm GTNN của biểu thức P = 3x + 2y + \(\frac{6}{x}+\frac{8}{y}\)
Ta có : P = \(3x+2y+\frac{6}{x}+\frac{8}{y}\)
\(\Rightarrow P=\left[\frac{6}{x}+\frac{3}{2}x\right]+\left[\frac{8}{y}+\frac{1}{2}y\right]+(\frac{3}{2})(x+y)\)
\(\Rightarrow6+4+\frac{3}{2}\cdot6\)
\(\Rightarrow A\ge19\)
Vậy Amin = 19 => x = 2 với y = 4

Không biết đúng k nữa:
\(2x^2+\frac{6}{x^2}+3y^2+\frac{8}{y^2}\)
\(=\left(2x^2+\frac{2}{x^2}\right)+\left(3y^2+\frac{3}{y^2}\right)+\left(\frac{4}{x^2}+\frac{5}{y^2}\right)\ge2\cdot2+3\cdot2+9=19\)
Vậy Min=19 khi x=y=1

Câu hỏi của KHANH QUYNH MAI PHAM - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo!


\(M=\frac{x-y+5\sqrt{x}-5\sqrt{y}}{\sqrt{x}+\sqrt{y}+5}=\frac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)+5\left(\sqrt{x}-\sqrt{y}\right)}{\sqrt{x}+\sqrt{y}+5}=\frac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}+5\right)}{\left(\sqrt{x}+\sqrt{y}+5\right)}=\sqrt{x}-\sqrt{y}\)
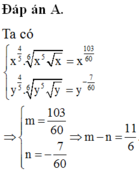
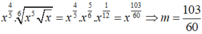
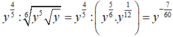
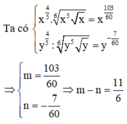
Đáp án là A