Trên mặt phẳng ta xét một hình chữ nhật với các điểm Một con châu chấu nhảy trong hình chữ nhật đó tính cả trên cạnh hình chữ nhật sao cho chân nó luôn đáp xuống mặt phẳng tại các điểm có tọa độ nguyên( tức là điểm có cả hoành độ và tung độ đều nguyên). Tính xác suất để nó đáp xuống các điểm mà
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
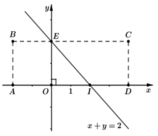
Để con châu chấu đáp xuống các điểm M(x; y) có x + y < 2 thì con châu chấu sẽ nhảy trong khu vực hình thang BEIA
Để M(x; y) có tọa độ nguyên thì x ∈ - 2 ; - 1 ; 0 ; 1 ; 2 , y ∈ { 0 ; 1 ; 2 }
Nếu x ∈ - 2 ; - 1 thì y ∈ { 0 ; 1 ; 2 } có 2.3 = 6 điểm
Nếu x = 0 thì y ∈ { 0 ; 1 } có 2 điểm
Nếu x =1 => y = 0 => có 1 điểm
=> có tất cả 6 + 2 + 1 = 9 điểm. Để con châu chấu nhảy trong hình chữ nhật mà đáp xuống các điểm có tọa độ nguyên thì x ∈ - 2 ; - 1 ; 0 ; 1 ; 2 ; 3 ; 4 , y ∈ { 0 ; 1 ; 2 } . Số các điểm M(x; y) có tọa độ nguyên là: 7.3 = 21 điểm. Xác suất cần tìm là: P = 9 21 = 3 7 .

Chọn C
Lời giải. Số các điểm có tọa độ nguyên thuộc hình chữ nhật là 7.3 = 21 điểm vì
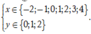
Để con châu chấu đáp xuống các điểm M(x,y) có x + y < 2
thì con châu chấu sẽ nhảy trong khu vực hình thang BEIA
Để M(x,y) có tọa độ nguyên thì
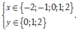
= Nếu x ∈ - 2 ; - 1 thì y ∈ 0 ; 1 ; 2
⇒ có 6 điểm
= Nếu x = 0 thì y ∈ 0 ; 1 ⇒ có 2 điểm
= Nếu x = 1 ⇒ y = 0 ⇒ có 1 điểm
⇒ có tất cả 6 + 2 +1 = 9 điểm thỏa mãn
Vậy xác suất cần tính P = 9 21 = 3 7

Đáp án A
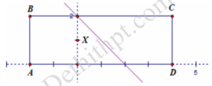
Đường thẳng x + y − 2 = 0 chia hình chữ nhật thành 2 phần như hình vẽ. Xét điểm X 0 ; 1
Số các điểm nguyên không nằm bên ngoài hình chữ nhật là 3.7 = 21 (điểm)
Các điểm có tọa độ thỏa mãn x + y < 2 là các điểm nằm phía bên trái đường thẳng x + y − 2 = 0 , hay cùng phía với X so với đường thẳng x + y − 2 = 0 và không lấy các điểm nằm trên đường thẳng này.
Dễ thấy trường hợp này có 9 điểm thỏa mãn
Vậy xác suất cần tìm là 9 21 = 3 7

Tham khảo:
a)
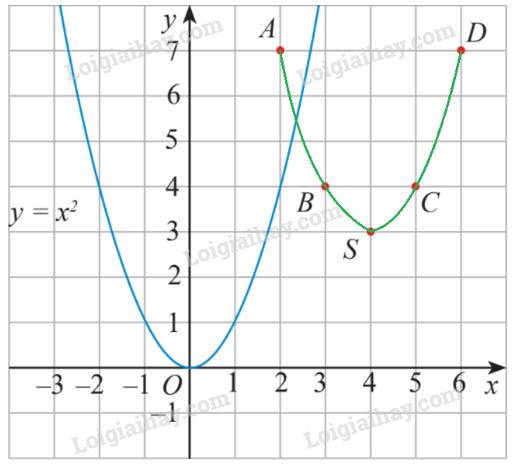
Đường cong đi qua 5 điểm này có cùng hình dạng với đồ thị hàm số \(y = {x^2}\), cùng có bề lõm quay lên trên.
b)
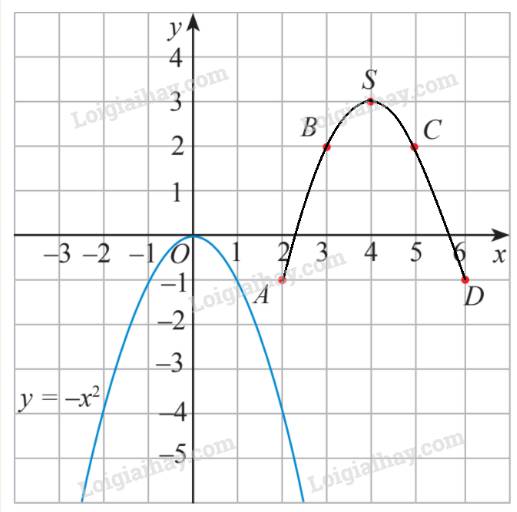
Đường cong đi qua 5 điểm này có cùng hình dạng với đồ thị hàm số \(y = - {x^2}\), cùng có bề lõm quay xuống dưới.


Đáp án A
Để con châu chấu đáp xuống các điểm M x , y có x + y < 2 thì con châu chấu sẽ nhảy trong khu vực hình thang BEIA
Để M x , y có tọa độ nguyên thì x ∈ − 2 ; − 1 ; 0 ; 1 ; 2 , y ∈ 0 ; 1 ; 2
Nếu x ∈ − 2 ; − 1 thì y ∈ 0 ; 1 ; 2 ⇒ có 2.3 = 6 điểm
Nếu x = 0 thì y ∈ 0 ; 1 ⇒ có 2 điểm
Nếu x = 1 ⇒ y = 0 ⇒ có 1 điểm
có tất cả 6 + 2 + 1 = 9 điểm. Để con châu chấu nhảy trong hình chữ nhật mà đáp xuống các điểm có tọa độ nguyên thì x ∈ − 2 ; − 1 ; 0 ; 1 ; 2 ; 3 ; 4 , y ∈ 0 ; 1 ; 2 ⇒
Số các điểm M x , y có tọa độ nguyên là: 7.3 = 21 điểm. Xác suất cần tìm là: P = 9 21 = 3 7 .