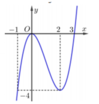
Cho hàm số có đồ thị như hình vẽ bên. Đồ thị hàm số có tổng tung độ của các điểm cực trị là?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
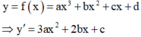
Nhìn vào đồ thị của hàm số y = f '(x) ta nhận thấy đồ thị hàm số đi qua các điểm (1;0), (3;0), (2;1) nên có hệ phương trình sau:
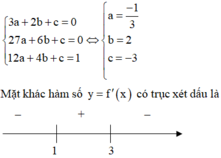
Nên đồ thị hàm số y = f(x) có điểm cực tiểu có tung độ bằng 2 3

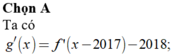
![]()
Dựa vào đồ thị hàm số y= f’(x) suy ra phương trình f’( x- 2017) = 2018 có 1 nghiệm đơn duy nhất.
Suy ra hàm số y= g( x) có 1 điểm cực trị

Chọn A
Ta có: g(x) = f(x-2017) - 2018x + 2019.
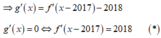
Nhận xét: tịnh tiến đồ thị hàm số y = f'(x) sang bên phải theo phương của trục hoành 2017 đơn vị ta được đồ thị hàm số y = f'(x-2017) . Do đó, số nghiệm của phương trình f'(x) = 2018 bằng số nghiệm của phương trình (*).
Dựa vào đồ thị ta thấy phương trình (*) có nghiệm đơn duy nhất hay hàm số đã cho có duy nhất 1 điểm cực trị.

Đáp án D
Ta có: y ' = 3 a x 2 + 2 b x + c
+) Đồ thị hàm số f'(x) đi qua gốc tọa độ => c=0
+) Đồ thị hàm số f'(x) có điểm cực trị:
1 ; − 1 ⇒ 6 a + 2 b = 0 3 a + 2 b = − 1 ⇔ a = 1 3 b = − 1
Vậy hàm số f ' x = x 2 − 2 x . Đồ thị hàm số f(x) tiếp xúc với trục hoành nên có cực trị nằm trên trục hoành. Các giá trị cực trị của hàm số f(x) là:
f 0 = d f 2 = 8 3 − 4 + d = − 4 3 + d
do điểm tiếp xúc có hoành độ dương
=> d = 4 3 => f(x) cắt trục tung tại điểm có tung độ 4 3
Đáp án B
Ta có đồ thị hàm số y = a − 2017 x 3 + b x 2 + c x + d + 4 (dịch chuyển hình đề bài lên trên 4 đơn vị) như hình 1
y = a − 2017 x 3 + b x 2 + c x + d + 4 như hình 2 (Dựa vào hình 1 để vẽ hình 2)
Tọa độ các điểm cực trị − 1 ; 0 , 0 ; 4 , 2 ; 0 ⇒ ∑ y = 4