Tìm tất cả các giá trị của tham số m để đồ thị hàm số cắt trục hoành tại bốn điểm phân biệt có các hoành độ thỏa mãn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trả lời :
Bn Do Phuong Mai đừng bình luận linh tinh nhé !
- Hok tốt !
^_^

Để hai đồ thi có điểm chung thì
\(-2x^2-2x+m+3=0\) có nghiệm
\(\Leftrightarrow4-4\cdot\left(-2\right)\left(m+3\right)>=0\)
\(\Leftrightarrow4+8m+24>=0\)
hay m>=-7/4

Chọn D.
![]() TXĐ: D = R.
TXĐ: D = R.
![]()
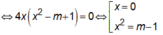
Đồ thị hàm số có 3 điểm cực trị ⇔ y' = 0 có ba nghiệm phân biệt ⇔ m -1 > 0 ⇔ m > 1(*)
3 điểm cực trị của đồ thị hàm số là: A(0;1),
Hàm số đã cho là hàm số chẵn nên đồ thị hàm số nhận Oy làm trục đối xứng
![]()
![]()
![]()
![]()
Ta có
![]()
![]()
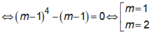
Kết hợp với điều kiện (*) => m = 2
Làm theo bào toán trắc nghiệm như sau:
Hàm số đã cho có 3 điểm cực trị khi ab < 0 ![]()
Chỉ có đáp án D thỏa mãn.

Đáp án A
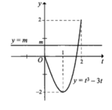
![]() (*)
(*)
Đặt ![]()
Yêu cầu bài toán trở thành: Tìm m để phương trình ![]() có nghiệm
có nghiệm ![]()
Từ đồ thị đã cho, ta suy ra đồ thị của hàm số ![]()
Từ đó ta có kể quả thỏa mãn yêu cầu bài toán ![]()

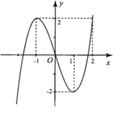
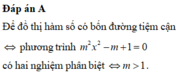
Đáp án D
PT hoành độ giao điểm là: