Cho hình lăng trụ ABC.A'B'C' có , AC = , BC = a, . Hình chiếu vuông góc của C' lên mặt phẳng (ABC) trùng với trung điểm M của AB. Tính góc tạo bởi đường thẳng C'M với mặt phẳng (ACC' A') ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
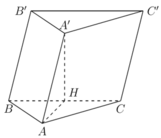
Gọi H là trung điểm của BC.
Ta có: B C = A B 2 + A C 2 = 2 a , A H = B C 2 = a
tam giác AA'H có A ' H = A A ' 2 - A H 2 = a 3
Vậy thể tích lăng trụ là V = A ' H . S A B C = a 3 . 1 2 . a 2 3 = 3 a 3 2

Đáp án B
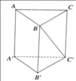
Ta thấy A ' . A B C là tứ diện đều cạnh a → V A ' . A B C = a 3 2 12
Vậy thể tích khối lăng trụ A B C . A ' B ' C ' là V = 3 × V A ' . A B C = 3. a 3 2 12 = a 3 2 4


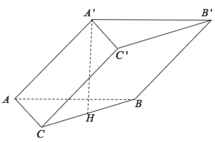
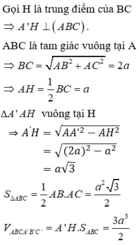
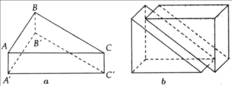

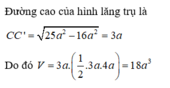
Chọn D
Trong (ABC), kẻ M N ⊥ A C ⇒ A C ⊥ ( M N C ' ) (điểm N thuộc cạnh AC)
Vậy NC’ là hình chiếu của MC’ trên mp (ACC’A’)
Góc giữa MC’ và mp(ACC’A’) là góc M C ' N ^
Ta có: A B 2 = A C 2 + B C 2 = 5 a 2 ⇒ A B = a 5 ⇒ A M = a 5 2
CM là đường trung tuyến của tam giác ABC, nên có:
C M 2 = C A 2 + C B 2 2 − A B 2 4 = a 2 4 ⇒ C M = a 2
Tam giác CMC’ vuông tại M, nên:
C ' M = C C ' 2 − C M 2 = a 6 4
Diện tích:
S Δ A M C = 1 2 S Δ A B C = a 2 4 = 1 2 M N . A C ⇒ M N = a 2 2
Xét tam giác vuông MC’N, có:
tan M C ' N ^ = M N M C ' = 1 3 ⇒ M C ' N ^ = 30 o