Trong không gian với hệ trục Oxyz, cho hai điểm M(0;-1;2), N(-1;1;3) Một mặt phẳng (P) đi qua M, N sao cho khoảng cách từ điểm K(0;0;2) đến mặt phẳng (P) đạt giá trị lớn nhất. Tìm tọa độ vectơ pháp tuyến của mặt phẳng (P).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Chọn B
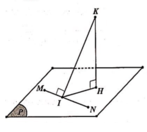
Gọi ![]() là vectơ pháp tuyến của (P) thỏa yêu cầu bài toán.
là vectơ pháp tuyến của (P) thỏa yêu cầu bài toán.
(P) qua N (-1; 0; -1) nên phương trình mặt phẳng có dạng:
A(x+1) + By + C(z+1) = 0 <=> Ax + By + Cz + A + C = 0
• (P) qua M (1;2;1) suy ra
A + 2B + C + A + C = 0 <=> A + B + C = 0 => A + C = - B (1)
• (P) cắt trục Ox tại A(a; 0; 0) suy ra A.a + A + C = 0 => A.a - B = 0 => a = B/A
(Do nếu A = 0 => B = 0 => C = 0 nên A ≠ 0). Suy ra A(B/A; 0; 0)
• (P) cắt trục Oy tại B (0; b; 0) suy ra B.b + A + C = 0 => B.b - B = 0 => B = 0 hoặc b = 1
TH1: B = 0 => A + C = 0. Chọn C = 1 => A = -1
Phương trình mặt phẳng (P) có dạng: x - z = 0 => A ≡ B ≡ O (0;0;0) => không thỏa yêu cầu.
TH2: b = 1 => B (0;1;0), 
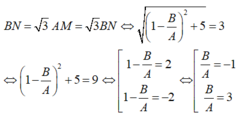
· B/A = -1 => B = -A => C = 0. Chọn A = 1 => B = -1
Phương trình mp (P): x - y + 1 = 0
· B/A = 3 => B = 3A => C = -4A. Chọn A = 1 => B = 3 => C = -4.
Phương trình mp (P): x + 3y - 4z - 3 = 0
Vậy có hai mặt phẳng thỏa yêu cầu.