Cho phương trình . Có bao nhiêu giá trị nguyên để phương trình đã cho có bốn nghiệm phân biệt?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: \(-2\le x\le2\)
Đặt \(\sqrt{x+2}+\sqrt{2-x}=t\Rightarrow\left\{{}\begin{matrix}2\le t\le2\sqrt{2}\\2\sqrt{-x^2+4}=t^2-4\end{matrix}\right.\)
Pt trở thành:
\(t+t^2-4+2m+3=0\)
\(\Leftrightarrow t^2+t-1=-2m\)
Xét hàm \(f\left(t\right)=t^2+t-1\) trên \(\left[2;2\sqrt{2}\right]\)
\(-\dfrac{b}{2a}=-\dfrac{1}{2}\notin\left[2;2\sqrt{2}\right]\)
\(f\left(2\right)=5\) ; \(f\left(2\sqrt{2}\right)=7+2\sqrt{2}\)
\(\Rightarrow5\le-2m\le7+2\sqrt[]{2}\)
\(\Rightarrow-\dfrac{7+2\sqrt{2}}{2}\le m\le-\dfrac{5}{2}\)
Có đúng 1 giá trị nguyên của m thỏa mãn là \(m=-4\)

Đặt t = x + 2 + 2 − x
Điều kiện t = x + 2 + 2 − x ≥ x + 2 + 2 − x = 2 ⇒ t ≥ 2
Lại có x + 2 + 2 − x ≤ 1 2 + 1 2 . x + 2 + 2 − x = 2 2 ⇒ t ≤ 2 2
Suy ra 2 ≤ t ≤ 2 2
Ta có: t 2 = 4 + 2 4 − x 2 ⇒ 2 4 − x 2 = t 2 − 4
Phương trình trở thành: t + t 2 − 4 − 2 m + 3 = 0 ⇔ t 2 + t − 2 m − 1 = 0
⇔ t 2 + t − 1 = 2 m *
Xét hàm số f ( x ) = t 2 + t − 1 (parabol có hoành độ đỉnh x = − 1 2 ∉ 2 ; 2 2 ) trên 2 ; 2 2 , có bảng biến thiên
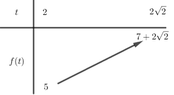
Phương trình (∗) có nghiệm thỏa 2 ≤ t ≤ 2 2 khi 5 ≤ 2 m ≤ 7 + 2 2
⇒ 5 2 ≤ m ≤ 7 + 2 2 2
5 2 ≤ m ≤ 7 + 2 2 2 → 2 , 5 ≤ m ≤ 4 , 91
Vậy có 2 giá trị m nguyên dương là m = 3 , m = 4
Đáp án cần chọn là: D

ĐK: \(-2\le x\le2\)
Đặt \(\sqrt{x+2}+\sqrt{2-x}=t\left(2\le t\le2\sqrt{2}\right)\)
Phương trình đã cho trở thành:
\(t+t^2-4+2m+3=0\)
\(\Leftrightarrow2m=f\left(t\right)=-t^2-t+1\)
Phương trình đã cho có nghiệm khi \(minf\left(t\right)\le2m\le maxf\left(t\right)\)
\(\Leftrightarrow-7-2\sqrt{2}\le2m\le-5\)
\(\Leftrightarrow\dfrac{-7-2\sqrt{2}}{2}\le m\le-\dfrac{5}{2}\)

Lời giải:
Để PT là PT bậc nhất 1 ẩn thì:
$m^2-m+1\neq 0$
$\Leftrightarrow (m-\frac{1}{2})^2+\frac{3}{4}>0$
Điều này luôn đúng với mọi $m\in\mathbb{R}$ do $(m-\frac{1}{2})^2+\frac{3}{4}\geq 0+\frac{3}{4}>0$ với mọi $m\in\mathbb{R}$
Vậy có vô số số thực $m$ thỏa mãn điều kiện đề.

\(\Delta=\left[-\left(m+3\right)\right]^2-4\left(2m+2\right)\\ =m^2+6m+9-8m-8\\ =m^2-2m+1\\ =\left(m-1\right)^2\)
de pt co 2 no pb thi Δ >0
<=> (m-1)^2>0
ma \(\left(m-1\right)^2\ge0\forall m\\ \Rightarrow\left(m-1\right)^2\ne0\\ \Leftrightarrow m\ne1\)
Viet: \(x1+x2=m+3\\ x1x2=2m+2\)
0<x1<x2<2\(\Rightarrow\left\{{}\begin{matrix}0< x1+x2< 4\\0< x1x1< 4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}0< m+3< 4\\0< 2m+2< 4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}-3< m< 1\\-1< m< 1\end{matrix}\right.\\ \Leftrightarrow-1< m< 1\)
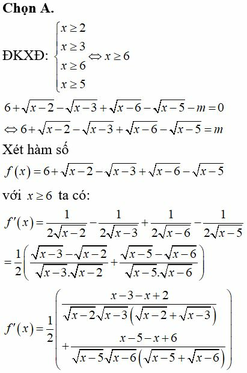


Chọn đáp án B
Phương trình tương đương với:
Đặt t = x 2 - 2 x + m , phương trình (1) đưa được về hệ:
Trừ theo vế của hai phương trình trong hệ trên, ta được:
Suy ra
Vẽ trên cùng một hệ trục tọa độ Oxy hai đường parabol P 1 : y = - x 2 + 3 x và P 2 : y = - x 2 + x + 1 (hình vẽ bên).
Xét phương trình hoành độ giao điểm của (P1) và (P2):
Suy ra (P1) cắt (P2) tại điểm 1 2 ; 5 4 .
Để phương trình đã cho có bốn nghiệm phân biệt
Đường thẳng y = m cắt (P1) tại hai điểm và cắt (P2) tại hai điểm.
Quan sát đồ thị ta thấy m ≤ 5 4 .
Vậy có 12 giá trị của m thỏa mãn yêu cầu bài toán.