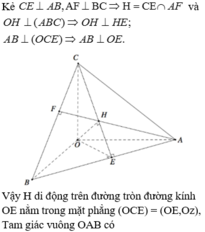
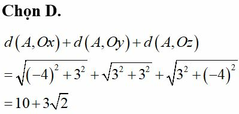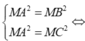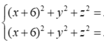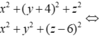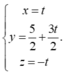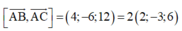Trong không gian Oxyz, cho ba điểm A(3;0;0),B(0;4;0),C(0;0;c) với c là số thực thay đổi khác 0. Khi c thay đổi thì trực tâm H của tam giác ABC luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn B
Gọi I là trung điểm của AB suy ra 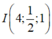 và (P) là mặt phẳng trung trực của đoạn AB.
và (P) là mặt phẳng trung trực của đoạn AB.
Mặt phẳng (P) đi qua I và nhận ![]() làm vec tơ pháp tuyến có phương trình là:
làm vec tơ pháp tuyến có phương trình là:
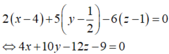
Gọi J là trung điểm của AC suy ra 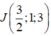 và (Q) là mặt phẳng trung trực của đoạn AC
và (Q) là mặt phẳng trung trực của đoạn AC
Mặt phẳng (Q) đi qua J và nhận ![]() làm vec tơ pháp tuyến có phương trình là:
làm vec tơ pháp tuyến có phương trình là:
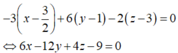
Khi đó d = (P) ∩ (Q)
Ta có d có vectơ chỉ phương ![]() và đi qua M là nghiệm của hệ
và đi qua M là nghiệm của hệ 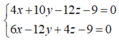 , ta chọn x = 4 suy ra y = 2 và z = 9/4. Vậy
, ta chọn x = 4 suy ra y = 2 và z = 9/4. Vậy 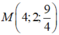
Phương trình tham số của d là: 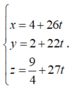

Đáp án A
A B → = 0 ; 4 ; 2 , A C → = − 3 ; 4 ; 3
A B C qua A 3 ; − 2 ; − 2 và có véc tơ pháp tuyến A B → , A C → = 4 ; − 6 ; 12 = 2 2 ; − 3 ; 6
⇒ A B C : 2 x − 3 y + 6 z = 0

Ta có: \(\overrightarrow{BC}=\left(-1;-6;3\right)\)
Đường thẳng song song với \(BC\) nên nó nhận \(\overrightarrow{BC}\) làm VTCP
\(\Rightarrow\) Phương trình tham số của đường thẳng đi qua \(A\) và song song với \(BC\) là: \(\left\{{}\begin{matrix}x=1-t\\y=-1-6t\\z=3+3t\end{matrix}\right.\quad\left(t\in R\right)\).