Tìm tất cả các số thực x, y để hai số phức z 1 = 9 y 2 - 4

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Pham Trong Bach

25 tháng 3 2019

Tìm tất cả các số thực x, y để hai số phức z 1 = 9 y 2 - 4 - 10 x i 5 , z 2 = 8 y 2 + 10 i 11 là hai số phức liên hợp của nhau. A. ...

Đọc tiếp

#Hỏi cộng đồng OLM #Mẫu giáo

Cao Minh Tâm

25 tháng 3 2019

Đúng(0)

Những câu hỏi liên quan

loancute

21 tháng 1 2021

1. Tìm tất cả các số tự nhiên $n$ để phân thức sau tối giản: $A=\dfrac{2n^2+3n+1}{3n+1}$

2. Cho các số thực dương x, y, z thỏa mãn $xy^2z^2+x^2z+y=3z^2$ .Tìm giá trị lớn nhất của biểu thức: $M=\dfrac{z^4}{1+z^4\left(x^4+y^4\right)}$

#Hỏi cộng đồng OLM #Toán lớp 9

Nguyễn Việt Lâm

Giáo viên

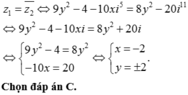
21 tháng 1 2021

Gọi $d=ƯC\left(2n^2+3n+1;3n+1\right)$

$\Rightarrow2n^2+3n+1-\left(3n+1\right)⋮d$

$\Rightarrow2n^2⋮d\Rightarrow2n\left(3n+1\right)-3.2n^2⋮d$

$\Rightarrow2n⋮d\Rightarrow2\left(3n+1\right)-3.2n⋮d\Rightarrow2⋮d\Rightarrow\left[{}\begin{matrix}d=1\\d=2\end{matrix}\right.$

$d=2\Rightarrow3n+1=2k\Rightarrow n=2m+1$

$\Rightarrow n$ lẻ thì A không tối giản

$\Rightarrow n$ chẵn thì A tối giản

Đúng(0)

Nguyễn Việt Lâm

Giáo viên

21 tháng 1 2021

Giả thiết tương đương:

$xy^2+\dfrac{x^2}{z}+\dfrac{y}{z^2}=3$

Đặt $\left(x;y;\dfrac{1}{z}\right)=\left(a;b;c\right)\Rightarrow a^2c+b^2a+c^2b=3$

Ta có: $9=\left(a^2c+b^2a+c^2b\right)^2\le\left(a^4+b^4+c^4\right)\left(c^2+a^2+b^2\right)$

$\Rightarrow9\le\left(a^4+b^4+c^4\right)\sqrt{3\left(a^4+b^4+c^4\right)}$

$\Rightarrow3\left(a^4+b^4+c^4\right)^3\ge81\Rightarrow a^4+b^4+c^4\ge3$

$\Rightarrow M=\dfrac{1}{a^4+b^4+c^4}\le\dfrac{1}{3}$

$M_{max}=\dfrac{1}{3}$ khi $\left(a;b;c\right)=\left(1;1;1\right)$ hay $\left(x;y;z\right)=\left(1;1;1\right)$

Đúng(2)

Quang Đẹp Trai

10 tháng 8 2023 - olm

Tìm tất cả các số thực dương x,y,z thỏa mãn :
$\left(1+\dfrac{x}{y+z}\right)^2+\left(1+\dfrac{y}{x+z}\right)^2+\left(1+\dfrac{z}{x+y}\right)^2=\dfrac{27}{4}$

#Hỏi cộng đồng OLM #Toán lớp 9

Akai Haruma

Giáo viên

10 tháng 8 2023

Lời giải:
Áp dụng BĐT Bunhiacopxky:

$\text{VT}(1^2+1^2+1^2)\geq (1+\frac{x}{y+z}+1+\frac{y}{x+z}+1+\frac{z}{x+y})^2$

$\Leftrightarrow 3\text{VT}\geq (3+\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y})^2$

$ = \left[3+\frac{x^2}{xy+xz}+\frac{y^2}{yz+yx}+\frac{z^2}{zy+zx}\right]^2$

$\geq \left[3+\frac{(x+y+z)^2}{2(xy+yz+xz)}\right]^2$

$\geq \left[3+\frac{3(xy+yz+xz)}{2(xy+yz+xz)}\right]^2=\frac{81}{4}$

$\Rightarrow \text{VT}\geq \frac{27}{4}$

Dấu "=" xảy ra khi $x=y=z>0$

Đúng(3)

Vũ Tuệ Lâm

10 tháng 8 2023

Áp dụng BĐT Bunhiacopxky:

$VT (1^{2} + 1^{2} + 1^{2}) \geq (1 + y + z x + 1 + x + z y + 1 + x + y z)^{2}$

$\Leftrightarrow 3 VT \geq (3 + y + z x + x + z y + x + y z)^{2}$

$= [3 + x y + x z x ^{2} + yz + y x y ^{2}$

Đúng(0)

Trần Ngọc Vy

15 tháng 12 2023 - olm

2. Tìm tất cả các số thực x, y, z thỏa mãn điều kiện 2sqrt(x) + 2sqrt(y - x) + 3sqrt(z - y) = 1/2 * (z + 17)

#Hỏi cộng đồng OLM #Toán lớp 9

violet

18 tháng 1 2022

a) $\dfrac{2x}{-9}$ = 10 phần 91

b) -5 phần 2x = 20 phần 28\

c) 1 phần 3 = -3x phần 36

bài 2

a)Tìm các số nguyên x, y sao cho : -4 phần = x phần 22 = 40 phần
b)Tìm các số nguyên x, y, z thỏa mãn: -4 phần 8 = x phần -10 = -7 phần y = z phần -24

#Hỏi cộng đồng OLM #Toán lớp 6

Nguyễn Lê Phước Thịnh

18 tháng 1 2022

a: =>-2x=90/91

hay x=-45/91

b: =>2x=-7

hay x=-7/2

c: ->-3x=-12

hay x=4

Đúng(0)

Nguyen Linh Nhi

10 tháng 4 2016 - olm

1) So sánh: A và B biết: A=8^9+12/8^9+7 và B=8^10+4/8^10-1

2) Cho A=1/2.3/4.5/6.7/8. ... .79/80. Chứng minh rằng: A<1/9

3) Thay a,b bởi các chữ số thích hợp để: 0,ab.(a+b)=0,36

4) Tìm các bộ số x,y,z thỏa mãn: x,y,z là các số nguyên tố và 1/x+1/y+1/z=1/8

#Hỏi cộng đồng OLM #Toán lớp 6

Thắng Nguyễn

10 tháng 4 2016

ta có:$A=\frac{8^9+12}{8^9+7}=\frac{8^9+7+5}{8^9+7}=\frac{8^9+7}{8^9+7}+\frac{5}{8^9+7}=1+\frac{5}{8^9+7}$

$B=\frac{8^{10}+4}{8^{10}-1}=\frac{8^{10}-1+5}{8^{10}-1}=\frac{8^{10}-1}{8^{10}-1}+\frac{5}{8^{10}-1}=1+\frac{5}{8^{10}-1}$

vì 8¹⁰-1>8⁹+7

$\Rightarrow\frac{5}{8^{10}-1}<\frac{5}{8^9+7}$

$\Rightarrow1+\frac{5}{8^{10}-1}<1+\frac{5}{8^9+7}$

=>A<B

Đúng(0)

Trần Trung Hiếu

12 tháng 5 2016

Chưa nghĩ ra...!!!

Đúng(0)

Lee Lynhh

7 tháng 1 2022

B1.Tìm x,y,z biết a.-10/15=x/9=-8/9=z/-21 b.x/21=8/y=40/z=4/3 B2.Cho biểu thức A=1/n-1 (Với n thuộc Z) a.Tìm điều kiện của n để A là phân số b.Tìm tất cả các giá trị nguyên của n để A là số nguyên B3.So sánh a.A=15 mũ 16+1/15 mũ 17+1 và B=15 mũ 15+1/15 mũ 16+1

#Hỏi cộng đồng OLM #Toán lớp 6

Nguyễn Lê Phước Thịnh

7 tháng 1 2022

Bài 2:

a: Để A là phân số thì n-1<>0

hay n<>1

b: Để A là số nguyên thì $n-1\in\left\{1;-1\right\}$

hay $n\in\left\{2;0\right\}$

Đúng(0)

Hồng Thanh

20 tháng 3 2019 - olm

Mọi người giúp mk với ạ :
Bài 1 : Cho các số thực dương x,y,z thỏa mãn x+y+z = 2019. Tìm giá trị nhỏ nhất của biểu thức P = 1/(x^2 +y^2 +z^2) +3/4xy + 3/4yz +3/4zx
Bài 2 : Tìm tất cả các bộ ba số nguyên tố (p;q;r) sao cho pqr = p+q+r+160
Bài 3 : Cho 8 đoạn thẳng có độ dài lớn hơn 10 và nhỏ hơn 210. Chứng minh rằng trong 8 đoạn thẳng đó luôn tìm đc 3 đoạn thẳng để ghép thành 1 tam giác.

#Hỏi cộng đồng OLM #Toán lớp 9

minh hue

12 tháng 11 2023 - olm

Bài 1: Tìm số nguyên χ biết:

a) (χ+3)(χ+2)=0

b) (7-3χ)³=(-8)

Bài 2: Tìm tất cả các số nguyên x;y;z;t biết:

|x+y+z+9|=|y+z+t+6|=|z+t+x-9|=|t+x+y-6|=0

Bài 3: Tìm ba cặp số nguyên (a;b) sao cho 20a+10b=2010

#Hỏi cộng đồng OLM #Toán lớp 6

Kiều Vũ Linh

12 tháng 11 2023

Bài 1

a) (x + 3)(x + 2) = 0

x + 3 = 0 hoặc x + 2 = 0

*) x + 3 = 0

x = 0 - 3

x = -3 (nhận)

*) x + 2 = 0

x = 0 - 2

x = -2 (nhận)

Vậy x = -3; x = -2

b) (7 - x)³ = -8

(7 - x)³ = (-2)³

7 - x = -2

x = 7 + 2

x = 9 (nhận)

Vậy x = 9

Đúng(1)

minh hue

12 tháng 11 2023

Thanks

Đúng(0)

violet

18 tháng 1 2022

a) 2x−92x−9 = 10 phần 91

b) -5 phần 2x = 20 phần 28\

c) 1 phần 3 = -3x phần 36

bài 2

a)Tìm các số nguyên x, y sao cho : -4 phần = x phần 22 = 40 phần
b)Tìm các số nguyên x, y, z thỏa mãn: -4 phần 8 = x phần -10 = -7 phần y = z phần -24

#Hỏi cộng đồng OLM #Toán lớp 8

Nguyễn Lê Phước Thịnh

18 tháng 1 2022

Bài 1:

a: =>2x-9=10/91

=>2x=829/91

hay x=829/182

b: =>2x=-7

hay x=-7/2

c: =>-3x=-12

hay x=4

Đúng(0)

Trang Hà

3 tháng 7 2015 - olm

1, Ba lớp 7A, 7B, 7C trồng được tất cả 1020 cây. Số cây lớp 7B trồng được bằng 8/9 số cây lớp 7A trồng được. Hỏi mỗi lớp trồng được bao nhiêu cây?

2, Tìm các số x, y, z biết: $\frac{x}{10}=\frac{y}{5};\frac{y}{2}=\frac{z}{3}$và 2x-3y+4z=330.

#Hỏi cộng đồng OLM #Toán lớp 6

Bùi Hoàng KHôi

4 tháng 8 2016

mình trả lời bài tìm x cho bạn nha

BCNN(5,2) =10

=)) x/20=y/10;y/10=z/15

=))x/20=y/10=z/15

x/20=y/10=z/15=2x/40=3y/30=4z/12

áp dụng dãy tính chất tỉ số bằng nhau ta có

2x/40=3y/30=4z/12=2x-3y+4z/40-30+12=330/22=15

x/20=15=))x=300

y/10=15=))y=150

z/15=15=))z=225

vậy x=300;y=150;z=225

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP