Cho mặt cầu và điểm A(2;0;1). Xét mặt phẳng (P) qua A, (P) tiếp xúc (S). Tìm một vecto pháp tuyến của (P).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mặt phẳng (P) có vec tơ pháp tuyến \(\overrightarrow{n}=\left(1;1;-2\right);\overrightarrow{AB}=\left(-2;1;-1\right)\)
Ta có \(\left[\overrightarrow{n};\overrightarrow{AB}\right]=\left(1;5;3\right)\)
(Q) vuông góc với (P), song song với đường thẳng AB suy ra (Q) có vectơ pháp tuyến là \(\left[\overrightarrow{n_1};\overrightarrow{AB}\right]=\left(1;5;3\right)\) nên phương trình mặt phẳng (Q) có dạng \(x+5y+3z+m=0\)
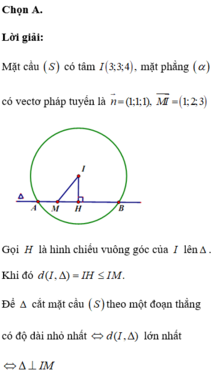
Mặt cầu (S) có tâm \(I\left(1;-1;1\right)\), bán kính R = 3
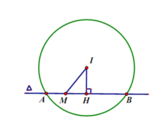
Mặt phẳng (Q) tiếp xúc với (S) có \(d\left(I,\left(Q\right)\right)=R\Leftrightarrow\frac{\left|1-5+3+m\right|}{\sqrt{35}}\)
\(\Leftrightarrow\left|m-1\right|=3\sqrt{35}\Leftrightarrow\begin{cases}m=1+3\sqrt{35}\\m=1-3\sqrt{35}\end{cases}\)
- Với \(m=1+3\sqrt{35}\) ta có phương trình mặt phẳng (Q) là : \(x+5y+3z+1+3\sqrt{35}=0\)
- Với \(m=1-3\sqrt{35}\) ta có phương trình mặt phẳng (Q) là : \(x+5y+3z+1-3\sqrt{35}=0\)











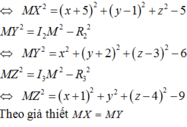


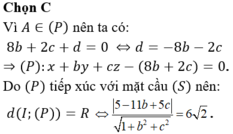
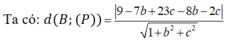
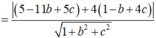
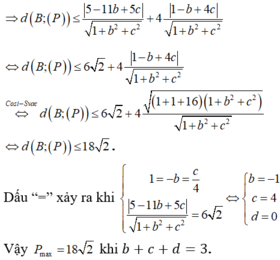
Chọn đáp án C