Trong không gian với hệ tọa độ Oxyz, cho và . Viết phương trình mặt phẳng (P) cách đều hai đường thẳng và .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B

Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).

Chọn A
Mặt phẳng qua I vuông góc với d có phương trình
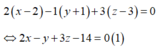
Gọi H là hình chiếu của I trên đường thẳng d.
Thay x, y, z từ phương trình của d vào (1) ta có


Đáp án A
Mặt phẳng qua I vuông góc với d có phương trình
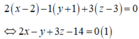
Gọi H là hình chiếu của I trên đường thẳng d.
Thay x, y, z từ phương trình của d vào ta có


Chọn A.
Gọi ∆ là đường thẳng cần tìm
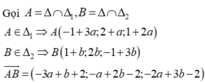
Đường thẳng d có vecto chỉ phương a d → = 0 ; 1 ; 1
![]()
![]()
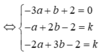
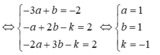
Ta có A(2;3;3); B(2;2;2)
∆ đi qua điểm A(2;3;3) và có vectơ chỉ phương ![]()
Vậy phương trình của ∆ là
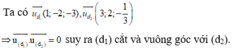



Đáp án B
Đường thẳng d 1 có vecto chỉ phương u 1 → = 1 ; 0 ; - 2 và M ( 1 ; - 3 ; 2 ) ∈ d 1
Đường thẳng d 2 có vecto chỉ phương u 2 → 1 ; - 2 ; 3 và N - 3 ; 1 ; - 4 ∈ d 2
Trung điểm MN là I(-1;-1;-1); u 1 → ∧ u 2 → = - 4 ; - 5 ; - 2
Mặt phẳng (P) cách đều 2 đường thẳng d 1 , d 2 khi (P) qua I(-1;-1;-1) và có vecto pháp tuyến n → = n 1 → ∩ n 2 →
⇒ ( P ) : - 4 ( x + 1 ) - 5 ( y + 1 ) - 2 z ( z + 1 ) = 0 ⇔ 4 x + 5 y + 2 z + 11 = 0