Chinh phục Đấu trường Tri thức OLM hoàn toàn mới, xem ngay!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
14 tháng 3 2019
Giá trị cực tiểu y C T của hàm số y = x + 4 x - 3 là. A. y C T = -3 B.  y C T = -1 C.  y C T ...
Đọc tiếp

Giá trị cực tiểu y C T của hàm số y = x + 4 x - 3 là.
#Hỏi cộng đồng OLM #Mẫu giáo
1
CM
Cao Minh Tâm
14 tháng 3 2019

Chọn D

Đúng(0)
PT
Pham Trong Bach
23 tháng 4 2018
Cho hàm số y = a x 3 + b x 2 + c x + d  đạt cực đại tại x = -2 với giá trị cực đại là 64; đạt cực tiểu tại x = 3 với giá trị cực tiểu là -61. Khi đó giá trị của a + b + c + d bằng A. 1 B. 7 C. -17 D. 5...
Đọc tiếp

Cho hàm số y = a x 3 + b x 2 + c x + d  đạt cực đại tại x = -2 với giá trị cực đại là 64; đạt cực tiểu tại x = 3 với giá trị cực tiểu là -61. Khi đó giá trị của a + b + c + d bằng
#Hỏi cộng đồng OLM #Mẫu giáo
1
CM
Cao Minh Tâm
23 tháng 4 2018

Ta có 64 = -8a + 4b - 2c + d; -61 = 27a + 9b + 3c +d

Từ y ' = 3 a x 2 + 2 b x + c  ta thu được hai phương trình 0 = 12a - 4b + c; 0 = 27a + 6b + c

Giải hệ gồm 4 phương trình trên ta thu được a = 2; b = -3; c = -36; d = 20 hay a + b + c + d = -17

Đáp án C

Đúng(0)
AS
An Sơ Hạ
24 tháng 9 2020

Câu 1 : Cho hàm số y = x2 +3 / x-1. Tìm cực tiểu của hàm số

Câu 2 : Gọi M,n lần lượt là giá trị cực đại, giá trị cực tiểu của hàm số y = x2 +3x+3 / x+2. Tính giá trị của biểu thức M2 - 2n ?

Câu 3 : Tìm giá trị cực đại ycđ của hàm số y = -x3 +2x2 -x+2

#Hỏi cộng đồng OLM #Toán lớp 12
0
MH
Minh Hảo Nguyễn Thị
31 tháng 8 2021
1,Tìm tất cả các giá trị của m để hàm số y=2x^2 - 3mx + m - 2 trên x-1 đạt cực đại tại điểm x=2. 2, Tìm tất cả các giá trị của m để hàm số y= x^2 + mx +1 trên x+m đạt cực tiểu tại điểm x=2. 3, Tìm tất cả các giá trị của m để hàm số y=x^2 -(2m-1)x+3 trên x+2 có cực đại và cực tiểu . 4, Tìm m để hso y=x^2 +m(m^2-1)x-m^4+1 trên x-m có cực đại và cực tiểu. Mọi người giúp em với ạ . Em...
Đọc tiếp

1,Tìm tất cả các giá trị của m để hàm số y=2x^2 - 3mx + m - 2 trên x-1 đạt cực đại tại điểm x=2. 2, Tìm tất cả các giá trị của m để hàm số y= x^2 + mx +1 trên x+m đạt cực tiểu tại điểm x=2. 3, Tìm tất cả các giá trị của m để hàm số y=x^2 -(2m-1)x+3 trên x+2 có cực đại và cực tiểu . 4, Tìm m để hso y=x^2 +m(m^2-1)x-m^4+1 trên x-m có cực đại và cực tiểu. Mọi người giúp em với ạ . Em cảm ơn ạ !
#Hỏi cộng đồng OLM #Toán lớp 12
0
PN
Phụng Nguyễn Thị
20 tháng 9 2020
Câu 1 : Tìm điều kiện m để hàm số y = \(\frac{1}{3}x^3+3x^2+mx-2\) có 2 điểm cực trị A. m \(\ge\) 9 B. m \(\le\) 9 C. m > 9 D. m < 9 Câu 2 : Tìm điểm cực tiểu của hàm số y = \(-x^3+3x^2+9x\) A. -5 B. 3 C. -1 D. 27 Câu 3 : Tính khoảng cách giữa hai điểm cực trị của đồ thị hàm số y = \(-x^3+3x^2\) A. \(2\sqrt{5}\) B....
Đọc tiếp

Câu 1 : Tìm điều kiện m để hàm số y = \(\frac{1}{3}x^3+3x^2+mx-2\) có 2 điểm cực trị

A. m \(\ge\) 9 B. m \(\le\) 9 C. m > 9 D. m < 9

Câu 2 : Tìm điểm cực tiểu của hàm số y = \(-x^3+3x^2+9x\)

A. -5 B. 3 C. -1 D. 27

Câu 3 : Tính khoảng cách giữa hai điểm cực trị của đồ thị hàm số y = \(-x^3+3x^2\)

A. \(2\sqrt{5}\) B. 6 C. 2 D. 8

Câu 4 : Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = \(x^3-12x+4\) có phương trình là :

A. y = 8x - 4 B. y = 2x - 1

C. y = -8x + 4 D. y = -2x + 1

Câu 5 : Gọi A, B là 2 điểm cực trị của đồ thị hàm số y = \(-2x^3+3x^2-2\) . Tính diện tích tam giác OAB

A. 2 B. 1 C. 3 D. 3/2

Câu 6 : Biết m = m0 thì giá trị cực đại của hàm số y = x3 - 3x + m -4 bằng 5 . Khoảng nào sau đây chứa m0 ?

A. (0;2) B. (2;4) C. (4;6) D. (6;8)

#Hỏi cộng đồng OLM #Toán lớp 12
2
PN
Phụng Nguyễn Thị
24 tháng 9 2020

Mọi người giải nhanh giúp mình mấy câu này với ạ

Đúng(0)
PN
Phụng Nguyễn Thị
25 tháng 9 2020

Mọi người giúp mình giải mấy câu này với ạ

Đúng(0)
PT
Pham Trong Bach
28 tháng 1 2018
Hàm số y =   a x 4 + b x 2 + c đạt cực đại tại A(0;-3) và đạt cực tiểu tại B(-1;-5). Khi đó, giá trị của a, b, c lần lượt là: A. 2;4;-3 B. -3;-1;-5 C. -2;4;-3 D. 2;-4;-3...
Đọc tiếp

Hàm số y =   a x 4 + b x 2 + c đạt cực đại tại A(0;-3) và đạt cực tiểu tại B(-1;-5). Khi đó, giá trị của a, b, c lần lượt là:
#Hỏi cộng đồng OLM #Mẫu giáo
1
CM
Cao Minh Tâm
28 tháng 1 2018

Đúng(0)
MM
Mint Mango
27 tháng 9 2021

Bài 4: Tìm giá trị của tham số m để hàm số: a) y=mx3 +mx2 −x+1 có cực đại, cực tiểu. b) y=x4 +(m−1)x2+1 có 3 cực trị.
#Hỏi cộng đồng OLM #Toán lớp 12
0
NH
Nguyễn Hạnh
13 tháng 7 2020
C1: y=[x²-(3m+2)x+m+4]/(x-1) Tìm m để hs có cực đại cực tiểu và khoảng cách giữa chúng của đths < 3 C2: y=[x³+mx+3]/(x+1) Tìm m để hs có cực đại cực tiểu, đồng thời 2đ CĐ,CT của đths nằm về 2 phía của đt (d): 2x+y-1=0 C3: y=[x²-(m+3)x+3m+1]/(x-1) Tìm m để hs có cực đại cực tiểu và giá trị của CĐ,CT cùng âm (Mn giải hộ e vs ạ, cần gấp lắm nên mong mn giúp đỡ)...
Đọc tiếp

C1: y=[x²-(3m+2)x+m+4]/(x-1)

Tìm m để hs có cực đại cực tiểu và khoảng cách giữa chúng của đths < 3

C2: y=[x³+mx+3]/(x+1)

Tìm m để hs có cực đại cực tiểu, đồng thời 2đ CĐ,CT của đths nằm về 2 phía của đt (d): 2x+y-1=0

C3: y=[x²-(m+3)x+3m+1]/(x-1)

Tìm m để hs có cực đại cực tiểu và giá trị của CĐ,CT cùng âm

(Mn giải hộ e vs ạ, cần gấp lắm nên mong mn giúp đỡ)

#Hỏi cộng đồng OLM #Toán lớp 12
0
PT
Pham Trong Bach
28 tháng 6 2018
Với giá trị nào của m, đồ thị hàm số y = x 3 – m x 2 + 3 ( m 2 - 1 ) x – m 3 + m  có điểm cực đại B, điểm cực tiểu C thỏa mãn OC = 3OB, với O là gốc tọa độ? A. m = 2 hoặc  m ...
Đọc tiếp

Với giá trị nào của m, đồ thị hàm số y = x 3 – m x 2 + 3 ( m 2 - 1 ) x – m 3 + m  có điểm cực đại B, điểm cực tiểu C thỏa mãn OC = 3OB, với O là gốc tọa độ?
#Hỏi cộng đồng OLM #Toán lớp 12
1
CM
Cao Minh Tâm
28 tháng 6 2018

Chọn A

Ta có  y ' = 3 x 2 - 6 m x + 3 ( m 2 - 1 ) .

Hàm số có hai cực trị => y' = 0 có hai nghiệm phân biệt <=> Δ' > 0 <=> ( 3 m ) 2 - 3 . 3 ( m 2 - 1 ) > 0 <=> 9 > 0 đúng với mọi m. Ta có điểm cực đại là B(m - 1; -2m + 2) và cực tiểu là C(m + 1; -2m - 2)

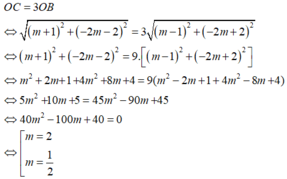
Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Đúng(0)
RO
Rơ Ông Ha Nhiêm
15 tháng 12 2017

Câu 1: Các điểm cực đại và cực tiểu của đồ thị hàm số \(y= x^4-2x^2+2\) tạo thành một tam giác có diện tích bằng

A.1 B.3 C.2 D.4

Câu 2: Tìm tất cả các giá trị của tham số m đẻ hàm số \(y=-(m^2+5m)x^3+6mx^2+6x-6 \) đạt cực đại tạ x=1

A. m=1 B.m=-2 C.m=-1 D.m=2
#Hỏi cộng đồng OLM #Toán lớp 12
2
AH
Akai Haruma
Giáo viên
17 tháng 12 2017

Câu 1:

Ta có: \(y=x^4-2x^2+2\Rightarrow y'=4x^3-4x=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)

Do đó 3 điểm cực trị của đồ thị hàm số là:

\(A(0;2);B(1;1);C(-1;1)\)

\(\Rightarrow \left\{\begin{matrix} AB=\sqrt{(0-1)^2+(2-1)^2}=\sqrt{2}\\ BC=\sqrt{(1--1)^2+(1-1)^2}=2\\ AC=\sqrt{(0--1)^2+(2-1)^2}=\sqrt{2}\end{matrix}\right.\)

Vì \(AB^2+AC^2=BC^2\) nên tam giác $ABC$ là tam giác vuông tại $A$

\(\Rightarrow S_{ABC}=\frac{AB.AC}{2}=\frac{\sqrt{2}.\sqrt{2}}{2}=1\)

Đáp án A

Đúng(0)
AH
Akai Haruma
Giáo viên
17 tháng 12 2017

Câu 2:

Để hàm số đạt cực trị tại $x=1$ thì:

\(y'=-3(m^2+5m)x^2+12mx+6=0\) tại $x=1$

hay \(-3(m^2+5m)+12m+6=0\)

\(\Leftrightarrow m^2+m-2=0\)

\(\Leftrightarrow m=1; m=-2\)

Với m=1:

Hàm số trở thành:

\(y=-6x^3+6x^2+6x-6\)

\(y'=-18x^2+12x+6=0\Leftrightarrow x=1; x=-\frac{1}{3}\)

Lập bảng biến thiên ta thấy thỏa mãn

Với m=-2

Hàm trở thành: \(y=6x^3-12x^2+6x-6\)

\(y'=18x^2-24x+6=0\Leftrightarrow x=1; x=\frac{1}{3}\)

Lập bảng biến thiên ta thấy tại $x=1$ đạt cực tiểu nên không thỏa mãn

Vậy m=1

Đáp án A

Đúng(0)
TL
thaoanh le thi thao
24 tháng 7 2017
cho h/s\(y=2x^3-3\left(m+1\right)x^{2+}6mx+m^3\). tìm m đẻ đồ thị hàm số có 2 điểm cực trị sao cho độ dài AB=\(\sqrt{2}\) 2. tìm m để đồ thị h/s \(y=x^4-2\left(m^2-m+1\right)x^2+m-1\) có 1 điểm cực đại , 2đ cực tiểu và thỏa mãn khoảng cách 2 điểm cực tiểu ngắn nhất 3. tìm m đẻ đồ thị h/s \(y=x^4-2mx^2+1\) có 3 điểm cực trị A( 0;1) , B,C thỏa mãn BC=4 4.cho h/s \(y=asinx+bcosx+x\) (\(0 x 2\Pi\)) đạt cực...
Đọc tiếp

cho h/s\(y=2x^3-3\left(m+1\right)x^{2+}6mx+m^3\). tìm m đẻ đồ thị hàm số có 2 điểm cực trị sao cho độ dài AB=\(\sqrt{2}\)

2. tìm m để đồ thị h/s \(y=x^4-2\left(m^2-m+1\right)x^2+m-1\) có 1 điểm cực đại , 2đ cực tiểu và thỏa mãn khoảng cách 2 điểm cực tiểu ngắn nhất

3. tìm m đẻ đồ thị h/s \(y=x^4-2mx^2+1\) có 3 điểm cực trị A( 0;1) , B,C thỏa mãn BC=4

4.cho h/s \(y=asinx+bcosx+x\) (\(0< x< 2\Pi\)) đạt cực trị tại x=\(\dfrac{\Pi}{3}\), x= \(\Pi\) tính tổng a+b

help me!
#Hỏi cộng đồng OLM #Toán lớp 12
5
金曜日 チャーターから
26 tháng 7 2017

lưa ý pt \(x^2=m^2-m+1\)có nghiệm với x phải #0 vì nếu = 0 thì trùng => sai

nhưng nghiệm \(\left(+,-\right)\sqrt{m^2-m+1}\)luôn #0 rồi khỏi lo

Đúng(0)
金曜日 チャーターから
25 tháng 7 2017

\(y'=6x^2-6\left(m+1\right)x+6m\)

ta có y/y'=\(\left(3m-1\right)x+m^3+m^2+m\)

suy ra y= \(\left(3m-1\right)x+m^3+m^2+m\)là pt của dường thẳng đi qua A và B

de-ta \(=9\left(m+1\right)^2-36m\)

y' có 2 \(n_o\)phân biệt khi m#1

hai hoành độ của hai điểm cực trị là :

\(X=\dfrac{-b\left(+,-\right)\sqrt{deta}}{a}=\)

\(\left[{}\begin{matrix}\dfrac{m+3}{2}\\\dfrac{3m-1}{2}\end{matrix}\right.\)<=>y=\(\left[{}\begin{matrix}2m^3+5m^2+10m+3\\2m^3+11m^2+4m+1\end{matrix}\right.\)(tìm y bằng cách thế x vào pt đường thẳng )

khoảng cách giữa hai điểm AB =\(\sqrt{2}\)

ta có pt : \(2=\left(\dfrac{m+3}{2}-\dfrac{3m-1}{2}\right)^2+\left(2m^3+5m^2+10m-3-\left(2m^3+11m^2-4m+1\right)\right)^2\)

lại sai chỗ nào rồi 0 ra nghiệm , cậu tính lại thử , cách giả là như vậy

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP