Question

[Pham Trong Bach]

Trong không gian với hệ tọa độ Oxyz, cho A(1;0;2), B(3;1;4), C(3;-2;1). Tìm tọa độ điểm S, biết SA vuông góc với (ABC), mặt cầu ngoại tiếp tứ diện S.ABC có bán kính bằng  $\frac{3\sqrt{11}}{2}$ và S có cao độ âm.

A. S(4;6;-4)

B.S(4;-6;-4)

C. S(-4;6;-4)

D. S(-4;-6;-4)

Answer 1

[Cao Minh Tâm]

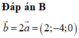
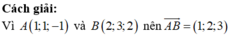
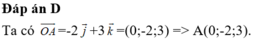
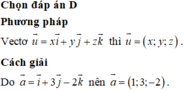
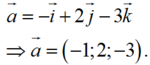
Chọn A.

Ta có 

Do SA vuông góc với (ABC) nên một VTCP của đường thẳng SA   được chọn là 

Đường thẳng SA qua A(1;0;2) và có VTCP  u → = ( 3 ; 6 ; - 6 )  nên có phương trình tham số là:

Gọi M là trung điểm BC khi đó M là tâm đường tròn ngoại tiếp tam giác ABC. Gọi d là đường thẳng qua M và song song với AS nên d ⊥ (ABC), suy ra d là trục đường tròn ngoại tiếp tam giác ABC.

Trong mặt phẳng (SAM) vẽ đường trung trực của SA cắt d tại I và cắt SA tại N.

Mặt phẳng (ABC) qua A và có một VTPT

 nên có phương trình tổng quát là:

mà cao độ của  S âm nên S(4;5;-4) thỏa yêu cầu bài toán.