Cho hàm số có đạo hàm Xét hàm số trên Trong các phát biểu sau:
(1) Hàm số đồng biến trên khoảng
(2) Hàm số nghịch biến trên khoảng
(3) Hàm số có 5 điểm cực trị.
(4)
Số phát biểu đúng là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có
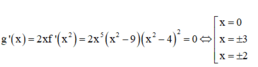
Bảng biến thiên của hàm số y= g( x)
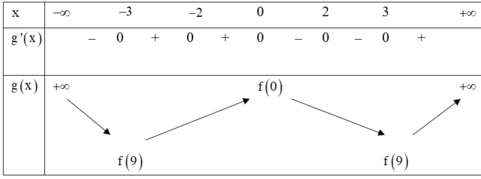
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng ( 3: + ∞) hàm số nghịch biến trong khoảng (-∞; -3) .
Hàm số có 3 cực trị, hàm số đạt giá trị nhỏ nhất tại x= ±3
Vậy có 3 khẳng định đúng là khẳng định I, II, IV
Chọn C.

Chọn D.
Xét g(x) = f x 2 - 2
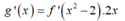
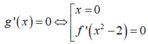
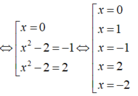
Bảng xét dấu g’(x):

Suy ra hàm số g(x) nghịch biến trên (-1;0) là sai.

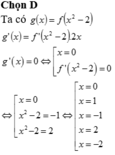
g’(x) đổi dấu qua các nghiệm đơn hoặc bội lẻ, không đổi dấu qua các nghiệm bội chẵn nên ta có bảng xét dấu g’(x)


Chọn D
Ta có g(x) = f( x 2 -2).
![]()
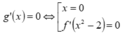
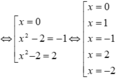
Ta có g'(3) = 6.f'(7) > 0, g’(x) đổi dấu qua các nghiệm đơn hoặc bội lẻ, không đổi dấu qua các nghiệm bội chẵn nên ta có bảng xét dấu g’(x):
![]()
Suy ra đáp án là D.
Đáp án B
Ta có g ' x = 2 x . f ' x 2 = 2 x . x 4 x 2 − 9 x 2 − 4 2
Suy ra g ' x đổi dấu khi đi qua 3 điểm x = 0 ; x = ± 3 ⇒ hàm số y = g x có 3 điểm cực trị
Mặt khác g ' x > 0 ⇔ − 3 < x < 0 x > 3 nên hàm số y = g x đồng biến trên khoảng − ∞ ; − 3 và − 3 ; 0
Hàm số y = g x nghịch biến trên khoảng − ∞ ; − 3 và 0 ; 3
Do x = 9 không phải điểm tới hạn của hàm số y = g x nên khẳng định 4 sai