Cho hàm số có đồ thị biểu diễn là đường cong (C) như hình vẽ. Khẳng định nào sau đây là sai?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án C.
Ta có h ' x = f ' x − g ' x = 0 ⇔ x = a x = b x = c .
Với x ∈ a ; b thì đồ thị g ' x nằm trên f ' x nên g ' x > f ' x ⇒ h ' x < 0 hàm số nghịch biến trên đoạn a ; b . Tương tự với x ∈ b ; c thì h x đồng biến.
Do đó M i n a ; c h x = h b .

Với hàm số y=f(-2x+1) có
![]()
![]()
![]()
Với hàm số y=g(ax+b) có
y'=a.g'(ax+b)>0 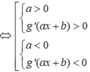
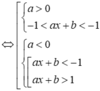
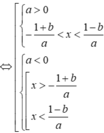
Vì hai hàm số đã cho có cùng khoảng đồng biến nên rơi vào trường hợp
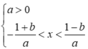 và
và 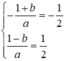
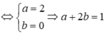
*Chú ý đồ thị đi lên hàm số đồng biến; đồ thị đi xuống hàm số nghịch biến.
Chọn đáp án C.

\(y'=2x-4\)
a.
\(y'\left(-2\right)=2.\left(-2\right)-4=-8\)
Phương trình tiếp tuyến:
\(y=-8\left(x+2\right)+15\Leftrightarrow y=-8x-1\)
b.
Gọi \(x_0\) là hoành độ tiếp điểm
\(\Rightarrow x_0^2-4x_0+3=3\Rightarrow x_0^2-4x_0=0\)
\(\Rightarrow\left[{}\begin{matrix}x_0=0\Rightarrow y'\left(0\right)=-4\\x_0=4\Rightarrow y'\left(4\right)=4\end{matrix}\right.\)
Có 2 tiếp tuyến: \(\left[{}\begin{matrix}y=-4\left(x-0\right)+3\\y=4\left(x-4\right)+3\end{matrix}\right.\) \(\Leftrightarrow...\)
c.
Gọi \(x_0\) là hoành độ tiếp điểm \(\Rightarrow y'\left(x_0\right)=k=4\)
\(\Rightarrow2x_0-4=4\Rightarrow x_0=4\)
\(\Rightarrow y\left(4\right)=3\)
Pttt: \(y=4\left(x-4\right)+3\Leftrightarrow y=4x-13\)

+ Ta có y ' = f ' ( x ) = a d - b c ( c x + d ) 2 . Từ đồ thị hàm số y= f’(x) ta thấy:
Đồ thị hàm số y= f’(x) có tiệm cận đứng x=1 nên –d/c= 1 hay c= -d
Đồ thị hàm số y= f’(x ) đi qua điểm (2;2)
⇒ a d - b c ( 2 c + d ) 2 = 2 ↔ a d - b c = 2 ( 2 c + d ) 2
Đồ thị hàm số y= f’(x) đi qua điểm (0;2)
⇒ a d - b c d 2 = 2 ↔ a d - b c = 2 d 2
Đồ thị hàm số y=f(x) đi qua điểm (0;3) nên b/d= 3 hay b= 3d
Giải hệ gồm 4 pt này ta được a=c= -d và b= 3d .
Ta chọn a=c= 1 ; b= -3 ; d= -1
⇒ y = x - 3 x - 1
Chọn D.

Điều kiện:


Từ đồ thị hàm số y=f(x) ta thấy phương trình f(x)=0 có nghiệm x=-3 (bội 2) và nghiệm đơn x = x 0 ∈ - 1 ; 0 nên ta viết lại f ( x ) = a x + 3 2 x - x 0
Khi đó

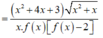
Dựa vào đồ thị ta cũng thấy, đường thẳng y=2 cắt đồ thị hàm số y=f(x) tại ba điểm phân biệt x=-1, x = x 1 ∈ - 3 ; - 1 , x = x 2 < - 3 nên ta viết lại
![]()
Khi đó
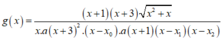
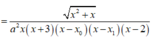
Dễ thấy x = x 0 ∈ - 1 ; 0 nên ta không xét giới hạn của hàm số tại điểm x 0
Ta có:
+) l i m x → 0 + g ( x ) = l i m x → 0 +
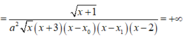
⇒ x = 0 là đường TCĐ của đồ thị hàm số y=g(x)
+) ![]()
⇒ Các đường thẳng x = - 3 , x = x 1 , x = x 2 đều là các đường tiệm cận đứng của đồ thị hàm số y=g(x)
Vậy đồ thị hàm số y=g(x) có tất cả 4 đường tiệm cận đứng.
Chọn đáp án D.