Cho mặt cầu (S) có phương trình x - 3 2 y 2 2 z

Trong không gian tọa độ Oxyz, cho A(-3;3;-3) thuộc mặt phẳng $(α)$ có phương trình 2x - 2y + z + 15 = 0 và mặt cầu (S): ${(x - 2)}^{2} + {(y - 3)}^{2} + {(z - 5)}^{2} = 100$ . Đường thẳng qua $∆$ , nằm trên mặt phẳng $(α)$ cắt (S) tại M, N. Để độ dài MN lớn nhất thì phương trình đường thẳng $∆$ là

A. $\frac{x + 3}{1} = \frac{y - 3}{4} = \frac{z + 3}{6}$

B. $\frac{x + 3}{16} = \frac{y - 3}{11} = \frac{z + 3}{- 10}$

C. $\{\begin{cases} x = - 3 + 5 t \\ y = 3 \\ z = - 3 + 8 t \end{cases}$

D. $\frac{x - 1}{3} = \frac{y - 3}{- 1} = \frac{z + 3}{3}$

#Hỏi cộng đồng OLM #Toán lớp 12

1

CM

Cao Minh Tâm

1 tháng 8 2019

Đúng(0)

PT

Pham Trong Bach

10 tháng 4 2018

Cho mặt cầu (S) có phương trình x − 3 2 + y + 2 2 + z − 1 2 = 100 và mặt phẳng α có phương...

Đọc tiếp

#Hỏi cộng đồng OLM #Mẫu giáo

1

CM

Cao Minh Tâm

10 tháng 4 2018

Đáp án A.

Đúng(0)

PT

Pham Trong Bach

30 tháng 1 2018

Trong không gian tọa độ Oxyz, cho mặt cầu (S) có phương trình (x-2)2 + (y+1)2 + (z-3)2 = 20. Mặt phẳng có phương trình x-2y+2z-1=0 và đường thẳng ∆ có phương trình x 1 = y + 2 2 = z + 4 - 30 ...

Đọc tiếp

#Hỏi cộng đồng OLM #Mẫu giáo

1

CM

Cao Minh Tâm

30 tháng 1 2018

Chọn D

Đúng(0)

PT

Pham Trong Bach

10 tháng 2 2018

Trong không gian Oxyz cho điểm M(2;1;1) mặt phẳng α : x+y+z-4=0 và mặt cầu (S): x - 3 2 + ( y - 3 ) 2 + ( z ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 12

1

CM

Cao Minh Tâm

10 tháng 2 2018

Đúng(0)

PT

Pham Trong Bach

12 tháng 1 2017

Trong không gian Oxyz cho điểm M (2;1;1), mặt phẳng α : x + y + z - 4 = 0 và mặt cầu ( s ) : ( x - 3 ) 2 + ( y - 3 ) ...

Đọc tiếp

#Hỏi cộng đồng OLM #Mẫu giáo

1

CM

Cao Minh Tâm

12 tháng 1 2017

Đúng(0)

PT

Pham Trong Bach

23 tháng 5 2019

Cho mặt cầu(S) có phương trình x - 3 2 + y + 2 2 + z - 1 2 = 100 và mặt phẳng (α) có phương trình 2x – 2y – z + 9 = 0....

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 12

1

CM

Cao Minh Tâm

23 tháng 5 2019

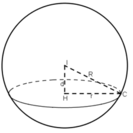
Giải bài 5 trang 92 sgk Hình học 12 | Để học tốt Toán 12

Từ phương trình x - 3 2 + y + 2 2 + z - 1 2 = 100 ta suy ra mặt cầu (S) có tâm I(3;-2;1) và có bán kính R=10. Gọi H là tâm cả đường tròn (C) - Hình chiếu vuông góc của I trên mặt phẳng ( α )

Phương trình tham số của đường thẳng IH là: x = 3 + 2 t y = - 2 - 2 t z = 1 - t Thay x,y,z từ phương trình tham số của đường thẳng IH vào phương trình mp α tại H(-1;2;3). H là tâm của đường tròn (C). Vậy bán kính của đường tròn (C) là