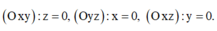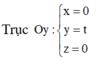Trong không gian Oxyz, cho điểm M(4;6;3). Qua M kẻ các tia Mx,My,Mz đôi một vuông góc. Ba điểm A,B,C lần lượt di động trên các tia Mx,My,Mz (không trùng với điểm M) sao cho điểm G(2; ;3) là trọng tâm tam giác ABC. Biết rằng I(a;b;c) là tâm mặt cầu ngoại tiếp tứ diện MABC. Giá trị biểu thức a+b+c bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án D
Phương pháp: (Oxy): z = 0, (Oyz): x = 0, (Oxz): y = 0
Trục Oy: x = 0 y = t z = 0
Cách giải: M (1;0;3) ∈ (Oxz)

Đáp án C
Gọi M(x; y; z). Ta có:
AM 2 + 2 BM 2 = x 2 + ( y - 2 ) 2 + ( z + 4 ) 2 + 2 [ ( x + 3 ) 2 + ( y - 5 ) 2 + ( z - 2 ) 2 ]
= x 2 + y 2 - 4y + 4+ z 2 +8z+ 16 + 2( x 2 + 6x + 9 + y 2 – 10y + 25 + z 2 – 4z + 4)
= 3(x2 + y2 + z2 + 4x - 8y) + 96 = 3[(x + 2)2 + (y - 4)2 + z2] + 36 ≥ 36
Dấu bằng xảy ra khi và chỉ khi x = -2, y = 4, z = 0 → M(-2; 4; 0).
Vậy đáp án đúng là C