Question

[Pham Trong Bach]

Cho biểu thức $A=\log \left(2017+\log \left(2016+\log \left(2015+\log \left(\mathrm{...}+\log \left(3+\log 2\right)\mathrm{...}\right)\right)\right)\right)$. Biểu thức A có giá trị thuộc khoảng nào trong các khoảng dưới đây?

A. $\left(\log 2017;\log 2018\right)$

B. $\left(\log 2018;\log 2019\right)$

C. $\left(\log 2019;\log 2020\right)$

D. $\left(\log 2020;\log 2021\right)$

Answer 1

[Cao Minh Tâm]

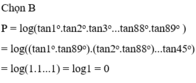
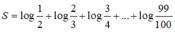
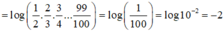
Đáp án D.

Dựa vào đáp án ta suy ra 3 < A < 4 .

  ⇒ 3 < log 2019 < A 2016 = log 2016 + A 2015 < log 2020 < 4

⇒ 3 < log 2020 < A 2017 = log 2017 + A 2016 < log 2021 < 4

Vậy A 2017 ∈ log 2020 ; log 2021 .