Biết rằng tổng S = 1 1 ! 2019 ! 1 3 ! 2017 ! 1 5 ! 2015 ! . . . ...

PT

Pham Trong Bach

8 tháng 7 2018

Biết rằng tổng S = 1 1 ! 2019 ! + 1 3 ! 2017 ! + 1 5 ! 2015 ! + . . . + 1 ...

Đọc tiếp

#Hỏi cộng đồng OLM #Mẫu giáo

1

CM

Cao Minh Tâm

8 tháng 7 2018

Đúng(0)

TH

Thị Hồng Nguyễn

5 tháng 4 2018 - olm

Tính :A= [(2018/1)+(2017/2)+(2016/3)+(2015/4)+...+(4/2015)+(3/2016)+(2/2017)+(1/2018)]/[(2019/2)+(2019/3)+(2019/4)+(2019/5)+...+(2019/2015)+(2019/2016)+(2019/2017)+(2019/2018)+(2019/2019)]

#Hỏi cộng đồng OLM #Toán lớp 7

0

MN

minh nguyen thuy

18 tháng 4 2020 - olm

Tính tổng: S = 2020 + 2019 – 2018 – 2017 + 2016 + 2015 – 2014 – 2013 + … + 4 + 3 – 2 – 1 . Vậy S = .................

#Hỏi cộng đồng OLM #Toán lớp 5

6

C

cat

18 tháng 4 2020

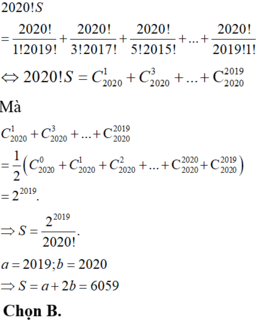
S = 2020 + 2019 - 2018 - 2017 + 2016 + 2015 - 2014 - 2013 + ... + 4 + 3 - 2 - 1

= ( 2020 + 2019 - 2018 - 2017 ) + ( 2016 + 2015 - 2014 - 2013 ) + ... + ( 4 + 3 - 2 - 1 ) (có tất cả 2020 : 4 = 505 nhóm)

= 4 + 4 + ... + 4

= 4. 505 = 2020

Vậy S = 2020.

Đúng(1)

-..-

18 tháng 4 2020

S= 2020

Bạn huyền đúng rồi đó .

hok tốt

Đúng(0)

TH

Thị Hồng Nguyễn

31 tháng 3 2018 - olm

Tính :A= [(2018/1)+(2017/2)+(2016/3)+(2015/4)+...+(4/2015)+(3/2016)+(2/2017)+(1/2018)]/[(2019/1)+(2019/2)+(2019/3)+(2019/4)+...+(2019/2015)+(2019/2016)+(2019/2017)+(2019/2018)+(2019/2019)]

#Hỏi cộng đồng OLM #Toán lớp 7

0

TM

Trà My Ngô Thị

25 tháng 12 2020

tính tổng S= (1/2018!)+(1/3!2016!)+(1/5!2014!)+...+(1/2017!2!)+(1/2019!)

#Hỏi cộng đồng OLM #Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

25 tháng 12 2020

\(S=\dfrac{1}{2018!\left(2019-2018\right)!}+\dfrac{1}{2016!\left(2019-2016\right)!}+...+\dfrac{1}{2!\left(2019-2\right)!}+\dfrac{1}{0!\left(2019-0!\right)}\)

\(\Rightarrow2019!.S=\dfrac{2019!}{2018!\left(2019-2018\right)!}+\dfrac{2019!}{2016!\left(2019-2016\right)!}+...+\dfrac{2019!}{2!\left(2019-2\right)!}+\dfrac{2019!}{0!\left(2019-0\right)!}\)

\(=C_{2019}^{2018}+C_{2019}^{2016}+...+C_{2019}^2+C_{2019}^0\)

\(=\dfrac{1}{2}\left(C_{2019}^0+C_{2019}^1+...+C_{2019}^{2018}+C_{2019}^{2019}\right)\)

\(=\dfrac{1}{2}.2^{2019}=2^{2018}\)

\(\Rightarrow S=\dfrac{2^{2018}}{2019!}\)

Đúng(1)

TN

trần nguyễn lan

6 tháng 2 2018

1) tìm x,y biết |x-y|+|y-z|+|z-x|=2017

2) so sánh a và b biết a=3^2017+5/3^2015+5

b=3^2015+1/3^2013+1

3) chứng minh rằng 24^54 . 54^24 . 2^10 chia hết cho 72^63

#Hỏi cộng đồng OLM #Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

18 tháng 6 2022

Bài 3:

\(24^{54}\cdot54^{24}\cdot2^{10}\)

\(=\left(2^3\cdot3\right)^{54}\cdot\left(3^3\cdot2\right)^{24}\cdot2^{10}\)

\(=2^{108}\cdot3^{54}\cdot3^{72}\cdot2^{24}\cdot2^{10}\)

\(=2^{142}\cdot3^{78}\)

\(72^{63}=\left(2^3\cdot3^2\right)^{63}=2^{189}\cdot3^{126}⋮2^{142}\cdot3^{78}\)(ĐPCM)

Đúng(0)

PN

pham nhu nguyen

1 tháng 10 2019 - olm

tính giá trị của tổng

D=1-2-3+4+5-6-7+8+....+2017-2018-2019+2020

C=1001 - 1003 + 1005 - 1007+...+ 2013 - 2015+2017

#Hỏi cộng đồng OLM #Toán lớp 6

2

NN

Nguyễn Ngọc Anh Minh

CTVHS VIP

1 tháng 10 2019

1/ D=(1-2-3+4)+(5-6-7+8)+...+(2017-2018-2019+2020)=0+0+...+0=0

Câu 2 ghép tương tự

Đúng(0)

PN

pham nhu nguyen

2 tháng 10 2019

ai có thể làm luôn câu C không ạ

Đúng(0)

YN

Yến Nhi

9 tháng 8 2016 - olm

3/1×2 + 3/3×5 + 3/5×7 + 3/7×9 +....+3/2015×2017+3/2017×2019

#Hỏi cộng đồng OLM #Toán lớp 5

1

SB

soyeon_Tiểu bàng giải

9 tháng 8 2016

Phân số đầu bn chép sai nhé, fai là 3/1x3 ms đúng

\(\frac{3}{1.3}+\frac{3}{3.5}+\frac{3}{5.7}+...+\frac{3}{2017.2019}\)

\(=\frac{3}{2}.\left(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{2017.2019}\right)\)

\(=\frac{3}{2}.\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{2017}-\frac{1}{2019}\right)\)

\(=\frac{3}{2}.\left(1-\frac{1}{2019}\right)\)

\(=\frac{3}{2}.\frac{2018}{2019}=\frac{1009}{673}\)

Dấu . là nhân

Đúng(0)

PT

Pham Trong Bach

3 tháng 8 2019

Tính các tổng sau

S = 1+3+5+…+2015+2017

A. S = 1018080

B. S = 1018081

C. S = 1018181

D. S = 1017072

#Hỏi cộng đồng OLM #Toán lớp 6

1

CM

Cao Minh Tâm

3 tháng 8 2019

Số số hạng của S là: (2017 -1): 2 + 1 = 1009

S = (2017 +1).1009: 2 =1018081

Đáp án cần chọn là B

Đúng(0)

DT

Dương Tấn Khôi

13 tháng 6 2020 - olm

bài toán: xét tổng gồm 2019 số hạng S= 5/1*2*3 + 8/2*3*4 + 11/3*4*5 +..... + 6053/2017*2018*2019

#Hỏi cộng đồng OLM #Toán lớp 8

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP