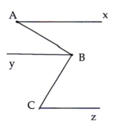
Cho hình vẽ bên, biết: x A B ^ = 30 O , A B C ^ = 90 O , By //Cz //Ax. Tính số đo B C z ^ .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
14 tháng 5 2018
Đúng(0)
Những câu hỏi liên quan
KV
30 tháng 8 2023
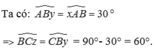
a) Vẽ tia By' là tia đối của tia By
Ta có:
∠ABy' + ∠ABy = 180⁰ (kề bù)
⇒ ∠ABy' = 180⁰ - ∠ABy
= 180⁰ - 135⁰
= 45⁰
⇒ ∠ABy' = ∠BAx = 45⁰
Mà ∠ABy' và ∠BAx là hai góc so le trong
⇒ By // Ax
b) Ta có:
∠CBy' = ∠ABC - ∠ABy'
= 75⁰ - 45⁰
= 30⁰
⇒ ∠CBy' = ∠BCz = 30⁰
Mà ∠CBy' và ∠BCz là hai góc so le trong
⇒ By // Cz
5 tháng 10 2021
\(a,Ax//By\Rightarrow\widehat{ABy}=\widehat{BAx}=120^0\left(so.le.trong\right)\\ b,\widehat{ABy}=\widehat{BCz}\left(=120^0\right)\)
Mà 2 góc này ở vị trí đồng vị nên \(By//Cz\)
Mà \(By//Ax\) nên \(Cz//Ax\)
Vậy có 3 cặp tia song song là \(Ax//By;By//Cz;Cz//Ax\)
Y
1
28 tháng 9 2021
\(a,\widehat{xAB}+\widehat{xAt}=180^0\left(kề.bù\right)\\ \Rightarrow\widehat{xAB}=180^0-60^0=120^0\\ \Rightarrow\widehat{xAB}=\widehat{yBA}\left(=120^0\right)\)
Mà 2 góc này ở vị trí so le trong nên \(Ax//By\)
\(b,\widehat{yBC}+\widehat{ABC}+\widehat{yBA}=360^0\\ \Rightarrow\widehat{yBC}=360^0-120^0-90^0=150^0\\ \Rightarrow\widehat{yBC}=\widehat{BCz}\left(=150^0\right)\)
Mà 2 góc này ở vị trí so le trong nên \(By//Cz\)
1 tháng 4 2022
\(2x-2y=by+cz-cz-ax=by-ax\)
\(\Rightarrow2x-2y=by-ax\)
\(\Rightarrow2x+ax=2y+by\)
\(\Rightarrow x\left(a+2\right)=y\left(b+2\right)\)
\(\Rightarrow a+2=\dfrac{y\left(b+2\right)}{x}\)
\(2z-2y=ax+by-cz-ax=by-cz\)
\(\Rightarrow2z+cz=2y+by\)
\(\Rightarrow z\left(c+2\right)=y\left(b+2\right)\)
\(\Rightarrow c+2=\dfrac{y\left(b+2\right)}{z}\)
\(A=\dfrac{2}{a+2}+\dfrac{2}{b+2}+\dfrac{2}{c+2}=\dfrac{2}{\dfrac{y\left(b+2\right)}{x}}+\dfrac{2}{b+2}+\dfrac{2}{\dfrac{y\left(b+2\right)}{z}}=\dfrac{2x}{y\left(b+2\right)}+\dfrac{2}{b+2}+\dfrac{2z}{y\left(b+2\right)}=\dfrac{2x}{y\left(b+2\right)}+\dfrac{2y}{y\left(b+2\right)}+\dfrac{2z}{y\left(b+2\right)}=\dfrac{2x+2y+2z}{y\left(b+2\right)}=\dfrac{by+cz+cz+ax+ax+by}{by+2y}=\dfrac{2\left(ax+by+cz\right)}{by+cz+ax}=2\)
XO
31 tháng 10 2021
Ta có ax + by = c ; by + cz = a
<=> cz - ax = a - c (1)
mà cz + ax = b (2)
Từ (1) và (2) => \(cz=\frac{a-c+b}{2}\Rightarrow z=\frac{a-c+b}{2c}\Rightarrow z+1=\frac{a+b+c}{2c}\)
=> \(\frac{1}{z+1}=\frac{2c}{a+b+c}\)
Tương tự ta có \(\frac{1}{x+1}=\frac{2a}{a+b+c}\); \(\frac{1}{y+1}=\frac{2b}{a+b+c}\)
=> P = \(\frac{1}{x+1}+\frac{1}{y+1}+\frac{1}{z+1}=\frac{2a}{a+b+c}+\frac{2b}{a+b+c}+\frac{2c}{a+b+c}=2\)
3 tháng 10 2021
a: \(ax+by+cz\)
\(=x^3-xyz+y^3-xyz+z^3-xyz\)
\(=x^3+y^3+z^3-3xyz\)