Cho khối chóp S.ABCD có ABCD là hình chữ nhật AD = 2a; AC = 3a. Gọi H là trọng tâm tam giác ABD. Biết SH vuông góc với mặt phẳng đáy. Góc giữa SA và bằng . Tính thể tích khối chóp S.ABCD ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có:
V S . A B C D = 1 3 S A . S A B C D = 1 3 .2 a . a .2 a = 4 3 a 3

Đáp án D
Diện tích hình chữ nhật ABCD là S = 2a2, chiều cao SA =a.
Vậy thể tích khối chóp S.ABCD là V = 1 3 . 2 a 2 . a = 2 3 a 3

Đáp án D
Ta có S A = S B 2 − A B 2 = 4 a
Khi đó:
V S . A B C D = 1 3 S A . S A B C D = 1 3 .4 a .6 a 2 = 8 a 3

Chọn C.
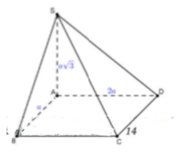
Ta có: SA ⊥ (ABCD)
ABCD là hình chữ nhật
S A B C D = A B . A D = a . 2 a = 2 a 2
Thể tích khối chóp S.ABCD là:
V S . A B C D = 1 3 S A B C D . S A = 1 3 2 a 2 . a 3 = 2 a 3 3 3

: Đáp án D
Thể tích khối chóp là: V = 1 3 S A . S A B C D = 1 3 a .2 a .3 a = 2 a 3 .
Đáp án C.
* Hướng dẫn giải:
Ta có
Ta có A H = 1 3 A C = a
Ta có A B = A C 2 - B C 2 = a 5
⇒ S A B C D = A B . A D = 2 a 5 2
⇒ V S . A B C D = 1 3 S H . S A B C D = 2 a 5 3 3