Question

[Pham Trong Bach]

Trong không gian Oxyz, cho điểm $M\left(\frac{59}{9};-\frac{32}{9};\frac{2}{9}\right)$ và mặt cầu $\left(S\right): {\left(x-1\right)}^2+{\left(y-2\right)}^2+{\left(z-3\right)}^2=25$. Từ điểm M kẻ các tiếp tuyến bất kỳ MA, MB, MC đến mặt cầu (S), trong đó A, B, C, D là các tiếp điểm. Tam giác ABC có diện tích lớn nhất bằng

A.  $12\sqrt{3}$

B. $24\sqrt{3}$

C. 16

D.  $\frac{27\sqrt{3}}{4}$

Answer 1

[Cao Minh Tâm]

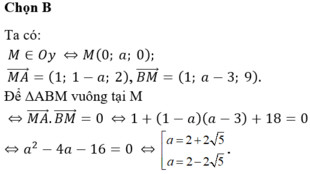
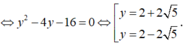
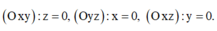
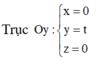
Chọn đáp án A.

Tiếp điểm của các tiếp tuyến kẻ từ M đến S) cùng thuộc một mặt phẳng và mặt phẳng này cắt (S) theo giao tuyến là đường tròn có tâm H và bán kính r

Như vậy, tam giác ABC nội tiếp đường tròn bán kính r = 4.