Cho A là tập tất cả các số tự nhiên có 4 chữ số phân biệt được lập từ tập {1;2;3;4;5;6;7;8;9}. Chọn ngẫu nhiên một số từ tập A. Xác suất để chọn được một số chia hết cho 11 và tổng bốn chữ số của nó chia hết cho 11 bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Vì là tập tất cả các số tự nhiên có 5 chữ số nên
![]()
![]()
![]()
Số phần tử của không gian mẫu là ![]()
Gọi X là biến cố: “Chọn được một số chia hết cho 7 và chữ số hàng đơn vị bằng 1 từ tập A”.
![]() có tận cùng bằng 1,do đó
có tận cùng bằng 1,do đó ![]() với
với ![]() có chữ số tận cùng là 3.
có chữ số tận cùng là 3.
Xét các trường hợp sau:
1) M là số có 4 chữ số có dạng
m
n
p
q
¯
Khi đó: ![]()
- Với m = 1, do ![]() và q = 3 nên n
≥
4
và q = 3 nên n
≥
4
+) Khi n = 4 thì p > 2 nên p ∈ {4;5;6;7;8;9}. Ta được 6 số thỏa mãn.
+) Khi n ≥ 5: Có 5 cách chọn n thuộc tập hợp {5;6;7;8;9}. Khi đó p ≠ m,n,q nên p có 7 cách chọn. Ta được 35 số thỏa mãn.
- Với m
≥
2 tức là có 7 cách chọn m từ tập {2;4;5;6;7;8;9}. Khi đó ![]() với mọi n,p thuộc tập hợp {0;1;2;4;5;6;7;8;9} và n
≠
p
≠
m, do đó có 8 cách chọn n, có 7 cách chọn p. Ta được 7.8.7 = 392 số thỏa mãn
với mọi n,p thuộc tập hợp {0;1;2;4;5;6;7;8;9} và n
≠
p
≠
m, do đó có 8 cách chọn n, có 7 cách chọn p. Ta được 7.8.7 = 392 số thỏa mãn
2) M là số có 5 chữ số có dạng m n p q r ¯ Khi đó: m n p q r ¯ ≤ 14285 và r = 3
Do m n p q r ¯ ≤ 14285 nên m chỉ nhận giá trị bằng 1 và n ≤ 4
- Với m=1; n = 0,2 thì p,q là các số tùy ý thuộc tập {0;2;4;5;6;7;8;9} và p ≠ q ≠ n Ta được 2.7.6 = 84 số thỏa mãn.
- Với m=1; n = 4:
+) Khi p = 0 thì q là số tùy ý thuộc tập {2;5;6;7;8;9}. Ta được 6 số thỏa mãn.
+) Khi p = 2 thì q phải thuộc tập {0;5;6;7;8}. Ta được 5 số thỏa mãn.
Vậy số phần tử của biến cố X là n(X) = 6 + 35 + 392 + 84 + 6 + 5 = 528
Xác suất để chọn được một số chia hết cho 7 và chữ số hàng đơn vị là 1 bằng
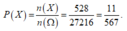

Đáp án D
Ta có bộ 3 số có tổng chia hết cho 3 là: {1;2;3}, {1;2;6}, {1;2;9}, {1;3;5}, {1;3;8}, {1;4;7}, {1;5;6},{1;5;9}, {1;6;8}, {1;8;9}, {2;3;4}, {2;3;7}, {2;4;6}, {2;4;9}, {2;5;8}, {2;6;7}, {2;7;9}, {3;4;5}, {3;4;8}, {3;5;7}, {3;6;9}, {3;7;8}, {4;5;6}, {4;5;9}, {4;6;8}, {5;6;7}, {6;7;8}, {7;8;9}.
Mỗi bộ số ta lập được 3! = 6 số.
Vậy có 30.6=180 số.

Đáp án D
Ta có bộ 3 số có tổng chia hết cho 3 là: {1;2;3}, {1;2;6}, {1;2;9}, {1;3;5}, {1;3;8}, {1;4;7}, {1;5;6},{1;5;9}, {1;6;8}, {1;8;9}, {2;3;4}, {2;3;7}, {2;4;6}, {2;4;9}, {2;5;8}, {2;6;7}, {2;7;9}, {3;4;5}, {3;4;8}, {3;5;7}, {3;6;9}, {3;7;8}, {4;5;6}, {4;5;9}, {4;6;8}, {5;6;7}, {6;7;8}, {7;8;9}.
Mỗi bộ số ta lập được 3!=6 số.
Vậy có 30.6=180 số.

Gọi chữ số cuối là x thì tổng 4 chữ số đầu là \(x+2\)
\(\Rightarrow\) Tổng 5 chữ số là: \(2x+2\)
Mặt khác tổng 5 chữ số nhỏ nhất từ tập đã cho là \(1+2+3+4+5=15\)
\(\Rightarrow2x+2\ge15\Rightarrow2x\ge13\)
\(\Rightarrow x=\left\{7;8;9\right\}\)
TH1: \(x=7\Rightarrow\) tổng 4 chữ số đầu là 9 mà \(1+2+3+4>9\Rightarrow\) không tồn tại 4 chữ số thỏa mãn
TH2: \(x=8\Rightarrow\) tổng 4 chữ số đầu bằng 10
Trong 9 chữ số, chỉ có duy nhất bộ \(\left\{1;2;3;4\right\}\) có tổng bằng 10
Do đó số số trong trường hợp này là: \(4!\) số
TH3: \(x=9\Rightarrow\) tổng 4 chữ số đầu bằng \(11\Rightarrow\) có 1 bộ 4 chữ số thỏa mãn là \(\left\{1;2;3;5\right\}\)
Trường hợp này cũng có \(4!\) số
Xác suất: \(P=\dfrac{4!+4!}{A_9^5}=...\)

Gọi số đó là \(\overline{abc}\)
Không gian mẫu: \(6.6.5=180\)
a. TH1: \(c=0\Rightarrow ab\) có \(A_6^2\) cách
TH2: \(c\ne0\Rightarrow c\) có 3 cách chọn, ab có \(5.5=25\) cách
Xác suất: \(P=\dfrac{3.25+A_6^2}{180}=\)
b. Tổng 3 chữ số chia hết cho 3 khi 3 số đồng dư khi chia 3 hoặc 3 số đôi một khác số dư khi chia 3.
- 3 số đồng dư khi chia cho 3: \(3!-2!=4\) số
- 3 số chia 3 có 3 số dư khác nhau:
+ Không có mặt số 0: \(C_2^1C_2^1C_2^1.3!=48\)
+ Có mặt số 0: \(C_2^1C_2^1C_2^1\left(3!-2!\right)=32\)
Xác suất: \(P=\dfrac{4+48+32}{180}=...\)

Chọn A
+ Ta có ![]()
![]()
Ta có d có 4 cách chọn {2;4;6;8}, a có 9 cách chọn, b có 9 cách chọn. Vì a + b + d khi chia cho 3 có 3 khả năng số dư
{0;1;2}, mà ![]() nên c có 3 cách chọn.
nên c có 3 cách chọn.
Ta có: ![]()
Xác suất cần tìm là: 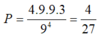


Chọn A
Số phần tử của A là A 9 4 = 3024 số.
Số phần tử của không gian mẫu là n ( Ω ) = 3024
Gọi A là biến cố: “Chọn được một số chia hết cho 11 và tổng bốn chữ số của nó chia hết cho 11”.
Xét số tự nhiên có 4 chữ số có dạng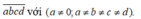
Theo bài ra ta có: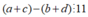 và
và 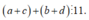
Suy ra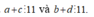
Trong các chữ số 1;2;3;4;5;6;7;8;9 có các bộ số mà tổng chia hết cho 11 là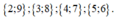
Chọn 2 cặp trong 4 cặp số trên để tạo số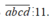
Chọn {a;c} có 4 cách, chọn {b;d} có 3 cách, sau đó sắp thứ tự các số a, b, c, d. Ta được 4.3.2.2 = 48
Suy ra n(A) = 48