Xác định giá trị của tham số m để hàm số sau không có cực trị
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


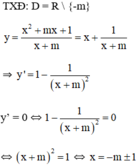
Ta có bảng biến thiên:
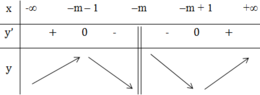
Dựa vào BBT thấy hàm số đạt cực đại tại x = -m – 1.
Hàm số đạt cực đại tại x = 2 ⇔ -m – 1 = 2 ⇔ m = -3.
Vậy m = -3.

Đáp án: A.
- Nếu m = 0 thì y = -2x - 2, hàm số không có cực trị.
- Nếu m ≠ 0: Hàm số không có cực trị khi và chỉ khi phương trình y' = m x 2 + 2mx + 2(m - 1) = 0 không có hai nghiệm phân biệt. Muốn vậy, phải có
Δ' = m 2 - 2m(m - 1) = - m 2 + 2m ≤ 0
⇔ 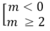

Đáp án: A.
- Nếu m = 0 thì y = -2x - 2, hàm số không có cực trị.
- Nếu m ≠ 0: Hàm số không có cực trị khi và chỉ khi phương trình y' = m x 2 + 2mx + 2(m - 1) = 0 không có hai nghiệm phân biệt. Muốn vậy, phải có
∆ ' = m 2 - 2m(m - 1) = - m 2 + 2m ≤ 0
⇔ 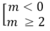

TXĐ: D = R
y’ = 3 x 2 + 4mx + m
Hàm số có cực trị khi và chỉ khi y’ đổi dấu trên R.
⇔ 3 x 2 + 4mx + m có hai nghiệm phân biệt.
⇔ Δ’ = 4 m 2 -3m > 0 ⇔ m(4m – 3) > 0
⇔ 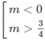
Vậy hàm số đã cho có cực đại, cực tiểu khi m < 0 hoặc m > 3/4.

TXĐ: D = R
y’ = 3 x 2 + 4mx + m
Hàm số có cực trị khi và chỉ khi y’ đổi dấu trên R.
⇔ 3 x 2 + 4mx + m có hai nghiệm phân biệt.
⇔ ∆ ’ = 4 m 2 -3m > 0 ⇔ m(4m – 3) > 0
⇔ 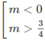
Vậy hàm số đã cho có cực đại, cực tiểu khi m < 0 hoặc m > 3/4.

Đáp án: C.
Tập xác định: D = R. y' = 3 x 2 - 6x + m.
Hàm số có cực trị khi và chỉ khi y' đổi dấu trên R
⇔ 3 x 2 - 6x + m = 0 có hai nghiệm phân biệt
⇔ ∆ ' = 9 - 3m > 0 ⇔ 3m < 9 ⇔ m < 3

Đáp án: C.
Tập xác định: D = R. y' = 3 x 2 - 6x + m.
Hàm số có cực trị khi và chỉ khi y' đổi dấu trên R
⇔ 3 x 2 - 6x + m = 0 có hai nghiệm phân biệt
⇔ Δ' = 9 - 3m > 0 ⇔ 3m < 9 ⇔ m < 3
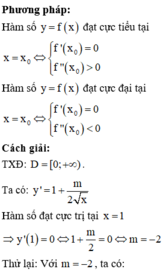
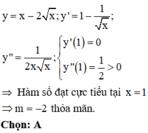
Hàm số không có cực trị khi đạo hàm của nó không đổi dấu trên tập xác định R\{m}.
Ta có:
Xét g(x) = x 2 – 2mx – 2 m 2 + 3
∆ ’g = m 2 + 2 m 2 – 3 = 3( m 2 – 1) ;
∆ ’g ≤ 0 khi – 1 ≤ m ≤ 1.
Khi – 1 ≤ m ≤ 1 thì phương trình g(x) = 0 vô nghiệm hay y’ = 0 vô nghiệm và y’ > 0 trên
tập xác định. Khi đó, hàm số không có cực trị.
Khi m = 1 hoặc m = -1, hàm số đã cho trở thành y = x + 3 (với x ≠ 1) hoặc y = x – 3 (với x ≠ - 1) Các hàm số này không có cực trị.
Vậy hàm số đã cho không có cực trị khi – 1 ≤ m ≤ 1.