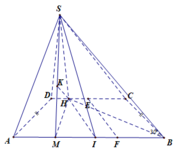
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, , mặt phẳng (SCD) vuông góc với mặt phẳng (ABCD). Tam giác ASI cân tại S, với I là trung điểm của cạnh AB, SB tạo với mặt phẳng (ABCD) một góc 30º. Khoảng cách giữa SI và CD là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A

ABCD là hình thanh cân có AB = BC = CD = a; AD = 2a nên M là tâm của đáy ABCD.
SA = AD = 2a; SA ⊥ (ABCD) => tam giác SAD vuông cân tại A nên tâm mặt cầu ngoại tiếp hình chóp S.ABCD là trung điểm N của SD
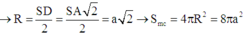

Đáp án B
Diện tích hình thang ABCD là:
S A B C D = A B . A D + B C 2 = 5
Vậy thể tích khối chóp S.ABCD là:
V = 1 3 . S A . S A B C D = 1 3 . S A . S A B C D = 1 3 .2.5 = 10 3 (đvtt)

Đáp án B.
Hướng dẫn giải:Ta có
![]()
Suy ra tam giác SAD vuông cân tại A nên SA = AD =2a .
Trong hình thang ABCD , kẻ B H ⊥ A D ( H ∈ A D ) .
Do ABCD là hình thang cân nên A H = A D - B C 2 = a 2 .
Tam giác AHB ,có B H = A B 2 - A H 2 = a 3 2
Diện tích S A B C D = 1 2 ( A D + B C ) . B H = 3 a 3 2 4 .
Vậy V S . A B C D = 1 3 S A B C D . S A = a 3 3 2
Đáp án D
Gọi M, E là trung điểm của AI và CD
Kẻ S H ⊥ C D do mặt phẳng (SCD) vuông góc với mặt phẳng
(ABCD) nên S H ⊥ ( A B C D ) . Mặt khác SA=SI
⇒ S M ⊥ A I ⇒ A I ⊥ ( S H M ) ⇒ H K ⊥ ( S A I ) mà CD
Song song với (SAB) ⇒ H K là khoảng cách cần tìm.
Qua E kẻ đường thẳng song song với BC cắt AB tại F
⇒ H B = a 3 ; S H = H B . tan 30 o = a 3 . 1 3 = a
Ta có 1 H K 2 = 1 S H 2 + 1 H M 2 = 1 a 2 + 4 3 a 2 = 7 3 a 2
⇒ H K = a 21 7