Trong không gian với hệ tọa độ Oxyz, cho mặt cầu và các điểm A(1;0;2), B(-1;2;2). Gọi (P) là mặt phẳng đi qua hai điểm A, B sao cho thiết diện của mặt phẳng (P) với mặt cầu (S) có diện tích nhỏ nhất. Khi viết phương trình (P) dưới dạng ax+by+cz+3=0. Tính tổng T=a+b+c
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Mặt cầu (S) có tâm I(a; b; c) và bán kính R thì có phương trình (x-a)²+(y-b)²+(z-c)²=R².
Theo đề bài ta có R²=9=> R=3.

Chọn A
Gọi ![]() là một vec tơ pháp tuyến của mặt phẳng (P).
là một vec tơ pháp tuyến của mặt phẳng (P).
Theo đề bài ta có mặt phẳng (P) vuông góc với mặt phẳng (α): x-y+z-4=0 nên ta có phương trình a-b+c=0 ó b=a+c ![]()
Phương trình mặt phẳng (P) đi qua A(0;1;2) và có véc tơ pháp tuyến là ax+ (a+c) (y-1)+c (z-2) =0
Khoảng cách từ tâm I (3;1;2) đến mặt phẳng (P) là 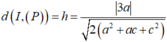
Gọi r là bán kính của đường tròn giao tuyến giữa mặt cầu (S) và mặt phẳng (P) ta có r²=16-h² ; r nhỏ nhất khi h lớn nhất.
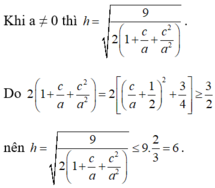
Dấu “=” xảy ra khi a = -2c. => một véc tơ pháp tuyến là ![]() => phương trình mặt phẳng (P) là 2x+y-z+1=0.
=> phương trình mặt phẳng (P) là 2x+y-z+1=0.
Vậy tọa độ giao điểm M của (P) và trục x'Ox là: 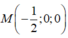


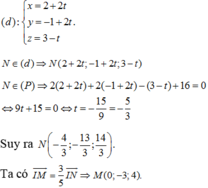

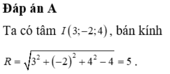
Đáp án B
Gọi J là hình chiếu vuông góc của I lên AB
A B → - 2 ; 2 ; 0 ⇒ A B : x = 1 - t y = t z = 2 J ∈ A B ⇒ J 1 - t ; t ; 2 ⇒ I J → - t ; t - 2 ; - 1 I J → . A B → = 0 ⇔ 2 t + 2 t - 4 = 0 ⇔ t = 1 ⇒ J ( 0 ; 1 ; 2 )
Thiết diện của (P) với (S) có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ I đến (P) lớn nhất khi và chỉ khi d(I;(P))=d(I;(AB)) =IJ
Vậy (P) là mặt phẳng đi qua J và có VTPT I J →
=> (P): x+(y-1)+(z-2)=0 <=> -x-y-z+3=0
=> T=-3