Trong không gian với hệ trục tọa độ Oxyz, cho và . Có bao nhiêu đường thẳng nằm trong mặt phẳng (P) mà và khoảng cách từ M đến bằng . Biết M là giao điểm của (P) và d.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B

Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).

Đáp án B
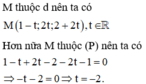
Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).

Đáp án D
Phương pháp:
Đường thẳng d: x - x 0 a = y - y 0 b = z - z 0 c có 1 VTCP là a → = a ; b ; c
Cách giải: Đường thẳng d có 1 VTCP là a → = 3 ; - 2 ; 1

Đáp án B.
Ta có: Hai vector chỉ phương của hai đường thẳng là cùng phương nên hai đường thẳng luôn đồng phẳng.
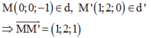
Vector chỉ phương của đường thẳng d là u → = ( 1 ; - 2 ; - 1 )
Vector pháp tuyến của mặt phẳng
![]()
Phương trình mặt phẳng
![]()


Đáp án A
Vì M là giao điểm của d và (P) nên ta có tọa độ của M cũng thỏa mãn phương trình mặt phẳng (P) hay
Gọi điểm H là hình chiếu của M lên đường thẳng △ ta có
Vậy tồn tại hai đường thẳng △ thỏa mãn đề bài.