Trong hệ tọa độ Oxyz cho A (3;3;0), B (3;0;3), C (0;3;3). Mặt phẳng (P) đi qua O, vuông góc với mặt phẳng (ABC) sao cho mặt phẳng (P) cắt các cạnh AB, AC tại các điểm M, N thỏa mãn thể tích tứ diện OAMN nhỏ nhất. Mặt phẳng (P) có phương trình: A. x+y-2z=0. B. x+y+2z=0. C. x-z=0. D. y-z=0...
Đọc tiếp
Trong hệ tọa độ Oxyz cho A (3;3;0), B (3;0;3), C (0;3;3). Mặt phẳng (P) đi qua O, vuông góc với mặt phẳng (ABC) sao cho mặt phẳng (P) cắt các cạnh AB, AC tại các điểm M, N thỏa mãn thể tích tứ diện OAMN nhỏ nhất. Mặt phẳng (P) có phương trình:
=(-7;6;10), nên 
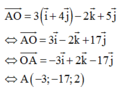
Chọn A
Nhận thấy tam giác ABC đều có trọng tâm G (2;2;2), và OG ⊥ (ABC) nên hình chiếu của O lên (ABC) là điểm G
Vì OG và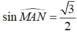
cố định nên thể tích 
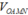nhỏ nhất khi và chỉ khi AM. AN nhỏ nhất.
Vì M, N, G thẳng hàng nên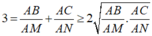
, suy ra 
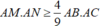. Đẳng thức xảy ra khi 
.
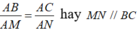Khi đó mặt phẳng (P) đi qua O và nhận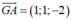
là một vectơ pháp tuyến, do đó (P): x+y-2z=0.