Chứng minh các dãy số là các cấp số nhân.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Với mọi ∀n ε N*, ta có (
. 2n+1) : (
. 2n) = 2.
Suy ra un+1 = un.2, với n ε N*
Vậy dãy số đã chp là một câp số nhân với u1 = , q = 2.
b) Với mọi ∀n ε N*, ta có un+1 = =un.
Vậy dãy số đã cho là một cấp số nhân với u1 = , q =
c) Với mọi ∀n ε N*, ta có un+1 = .

\(u_n=\dfrac{n^2+1}{2n^2-3}\)
\(=\dfrac{1}{2}\cdot\dfrac{n^2+1}{n^2-1,5}\)
\(=\dfrac{1}{2}\left(\dfrac{n^2-1,5+2,5}{n^2-1,5}\right)=\dfrac{1}{2}\left(1+\dfrac{2.5}{n^2-1,5}\right)< \dfrac{1}{2}\)
=>(Un) là dãy số bị chặn

a) Ta có:
\(\frac{{{u_n}}}{{{u_{n - 1}}}} = \frac{{ - \frac{3}{4}{{.2}^n}}}{{ - \frac{3}{4}{{.2}^{n - 1}}}} = \frac{{{2^n}}}{{{2^{n - 1}}}} = {2^1} = 2\)
Dãy số là cấp số nhân
b) Ta có: \(\frac{{{u_n}}}{{{u_{n - 1}}}} = \frac{{\frac{5}{{{3^n}}}}}{{\frac{5}{{{3^{n - 1}}}}}} = {3^{ - 1}} = \frac{1}{3}\)
Dãy số là cấp số nhân
c) Ta có: \(\frac{{{u_n}}}{{{u_{n - 1}}}} = \frac{{{{\left( { - 0,75} \right)}^n}}}{{{{\left( { - 0,75} \right)}^{n - 1}}}} = {\left( { - 0,75} \right)^{ - 1}} = - \frac{4}{3}\)
Dãy số là cấp số nhân

Các số hạng trong dãy này có dạng là \(\dfrac{n\left(n+1\right)}{2}\)
Tổng của hai số hạng liên tiếp trong dãy là:
\(\dfrac{n\left(n+1\right)+\left(n+1\right)\left(n+2\right)}{2}=\dfrac{n^2+n+n^2+3n+2}{2}=\dfrac{2n^2+4n+2}{2}\)
\(=n^2+2n+1\)
\(=\left(n+1\right)^2\) là số một số chính phương(đpcm)
⇒ (un) là cấp số nhân với công bội q = 2.
⇒ (un) là cấp số nhân với công bội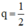
⇒ (un) là cấp số nhân với công bội