Trong không gian với hệ tọa độ Oxyz, xét đường thẳng Δ đi qua điểm A (0;0;1) và vuông góc với mặt phẳng Ozx. Tính khoảng cách nhỏ nhất giữa điểm B (0; 4; 0) tới điểm C trong đó C là điểm cách đều đường thẳng Δ và trục Ox
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A

Gọi I = d ∩ Δ. Do I ∈ Δ nên I (2t + 1; t – 1; -t).

từ đó suy ra d có một vectơ chỉ phương là ![]() và đi qua M (2 ; 1 ; 0) nên có phương trình
và đi qua M (2 ; 1 ; 0) nên có phương trình 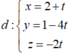

Chọn A.
Mặt phẳng (P) có vectơ pháp tuyến ![]()
Vì ∆ vuông góc với (P) nên d có vectơ chỉ phương ![]()
∆ đi qua điểm M(-2;1;1) và có vectơ chỉ phương u ∆ →
Vậy phương trình chính tắc của ∆ là x + 2 2 = y - 1 - 1 = z - 1 1

Chọn C
Gọi giao điểm của Δ và d là B nên ta có: B (3+t;3+3t;2t) ![]()
Vì đường thẳng Δ song song với mặt phẳng (α) nên:
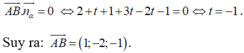
Phương trình đường thẳng Δ đi qua A và nhận 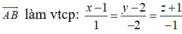

Đáp án A
Phương pháp:
Tính khoảng cách từ 1 điểm M đến đường thẳng Δ: 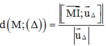 với
u
△
→
là 1 VTCP của Δ và I
∈
Δ là 1 điểm bất kì
với
u
△
→
là 1 VTCP của Δ và I
∈
Δ là 1 điểm bất kì
Cách giải: Đường thẳng Δ nhận ![]() là 1 VTCP
là 1 VTCP
Gọi M(a;b;0)
∈
(Oxy) => 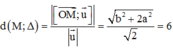
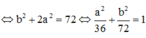
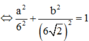
Như vậy tập hợp các điểm M là elip có phương trình 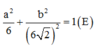
![]()



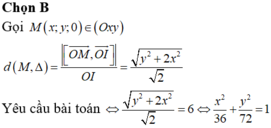



Chọn A
Vì đường thẳng Δ đi qua điểm A (0;0;1) và vuông góc với mặt phẳng Ozx thì Δ song song với trục Oy và nằm trong mặt phẳng Oyz. Dễ thấy OA là đường vuông góc chung của Δ và Ox
Xét mặt phẳng (α) đi qua I (0;0;1/2) và là mặt phẳng trung trực của OA.
Khi đó Δ // (α), Ox // (α) và mọi điểm nằm trên (α) có khoảng cách đến Δ và Ox là bằng nhau.
Vậy tập hợp điểm C là các điểm cách đều đường thẳng Δ và trục Ox là mặt phẳng (α). Mặt phẳng (α) đi qua I (0;0;1/2) có véc tơ pháp tuyến là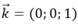 nên có phương trình:
nên có phương trình: 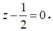
Đoạn BC nhỏ nhất khi C là hình chiếu vuông góc của B lên (α). Do đó khoảng cách nhỏ nhất giữa điểm B (0;4;0) tới điểm C chính là khoảng cách từ B (0;4;0) đến mặt phẳng (α):