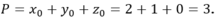Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (2; -3; 7), B (0; 4; -3) và C (4; 2; 5). Biết điểm M x 0 ; y 0 ; z 0 nằm trên (Oxy) sao cho M A → + M B → + M C → có giá trị nhỏ nhất. Khi đó tổng P = x 0 + y 0 + z 0 bằng:
A. P = 0
B. P = 6
C. P = 3
D. P = -3
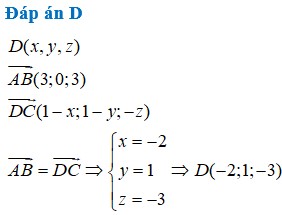
Chọn C
Gọi G là trọng tâm tam giác ABC => G = (2; 1; 3)
Khi đó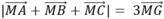
Nên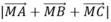
có giá trị nhỏ nhất khi và chỉ khi MG ngắn nhất, khi đó M là hình chiếu vuông góc của G (2; 1; 3) trên (Oxy)
Do đó M (2; 1; 0).
Vậy