Trong không gian Oxyz, cho mặt phẳng (P): 2x - y - 2z - 12 = 0 và hai điểm A ( 1;1;3 ), B ( 2;1;4 ). Tìm tập hợp tất cả các điểm sao cho tam giác ABC có diện tích nhỏ nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điểm cần tìm M(x;y;z) ta có điều kiện cách đều hai mặt phẳng là
![]()
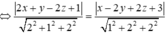
![]()
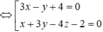
Vậy tập hợp các điểm này nằm trên hai mặt phẳng vuông góc với nhau (hai mặt phẳng này được gọi là mặt phẳng phân giác của góc tạo bởi hai mặt phẳng).
Chọn đáp án C.
Chọn đáp án C.

Đáp án A
Khoảng cách nhỏ nhất giữa hai điểm A và B chính là khoảng cách giữa hai mặt phẳng (P) và (Q), dấu bằng xày ra khi và chỉ khi AB vuông góc với (P). Mặt khác vì O thuộc (P) nên ta có:
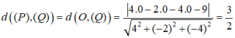
Vậy khoảng cách giữa hai điểm A và B nhỏ nhất bằng 3/2

Đáp án A
Hai mặt phẳng (P) và (Q) có cùng vecto pháp tuyến là: n → (2; -1; -2)
Điểm A(-3; 1; 0) thuộc mặt phẳng (P) nhưng không thuộc mặt phẳng (Q).
Do đó, hai mặt phẳng (P) và (Q) song song với nhau.
Khoảng cách giữa hai mặt phẳng là:
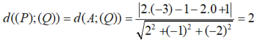
Vì mặt cầu (S) tiếp xúc với cả hai mặt phẳng (P) và (Q) nên khoảng cách giữa hai mặt phẳng (P) và (Q) chính là đường kính của mặt cầu: 2R = 2 nên R = 1.
Diện tích của mặt cầu (S) là: S = 4π R 2 = 4 π







Từ phương trình mặt phẳng (P) ta có: y = 2x - 2z - 12 nên tọa độ điểm C a ; 2 a - 2 b ; b
Ta có A B ⇀ = 1 ; 0 ; 1 , A C → = a - 1 ; 2 a - 2 b - 13 ; v - 3
Suy ra A B ⇀ , A C ⇀ = 2 a - 2 b - 13 ; b - a - 2 ; 13 - 2 a + 2 b
Do đó
S A B C = 1 2 A B ⇀ , A C ⇀ = 1 2 2 a - 2 b - 13 2 + b - a - 2 2 + 13 - 2 a + 2 b 2
Đặt t = a - b thì
4 S ∆ A B C 2 = 2 t - 13 2 + t + 2 2 + 13 - 2 t 2 = 9 t 2 - 100 t + 342 = 30 t - 50 3 2 + 578 9 ≥ 578 9
Dấu “=” xảy ra khi và chỉ khi t = 50 9
Do đó m i n S A B C = 17 2 6 khi t = 50 9 . Vì thế b = a - 50 9
Suy ra C a ; - 8 9 ; a - 50 9
Vậy tập hợp các điểm C là đường thẳng có phương trình x = t y = - 8 9 z = - 8 9 + t
Đáp án B